Simplify the expression: (x^3y^2)(xy^5)
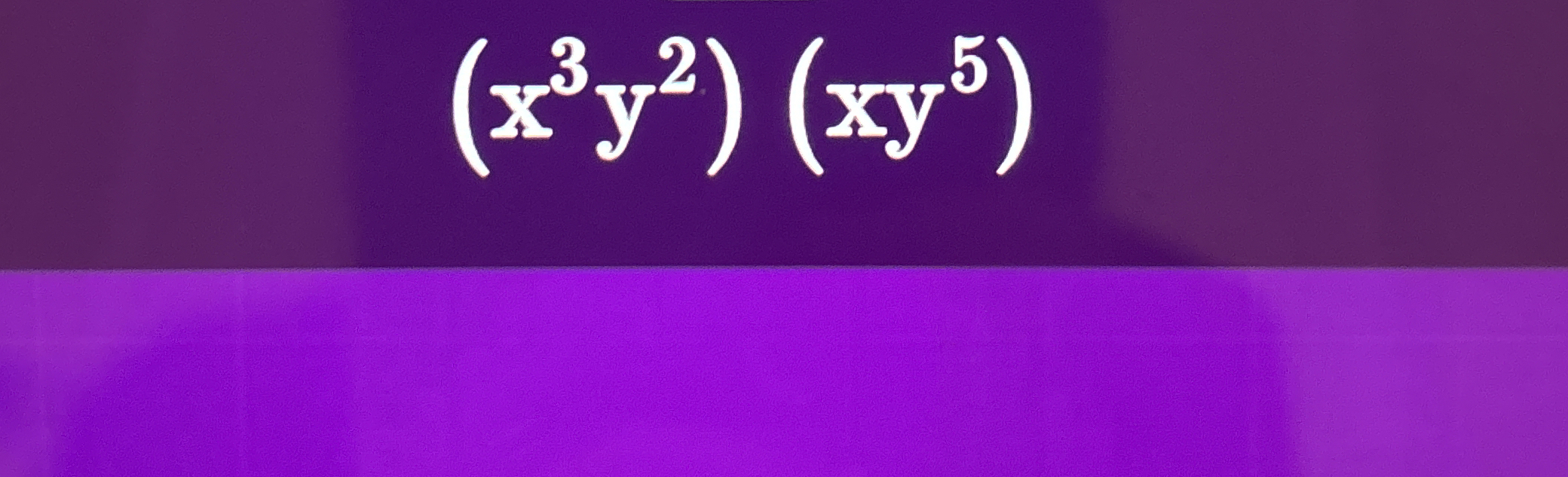
Understand the Problem
The question requires simplifying the given algebraic expression. We need to multiply the two terms by applying the exponent rules, particularly for terms with the same base.
Answer
$x^4y^7$
Answer for screen readers
$x^4y^7$
Steps to Solve
-
Rewrite the expression The given expression is $(x^3y^2)(xy^5)$.
-
Group like terms Group the $x$ terms and the $y$ terms together: $x^3 \cdot x \cdot y^2 \cdot y^5$.
-
Apply the exponent rule $x^a \cdot x^b = x^{a+b}$ to the $x$ terms $x^3 \cdot x = x^{3+1} = x^4$.
-
Apply the exponent rule $x^a \cdot x^b = x^{a+b}$ to the $y$ terms $y^2 \cdot y^5 = y^{2+5} = y^7$.
-
Combine the simplified $x$ and $y$ terms Multiply the simplified $x$ and $y$ terms together: $x^4y^7$.
$x^4y^7$
More Information
The simplified form of the given expression $(x^3y^2)(xy^5)$ is $x^4y^7$. This is obtained by multiplying the terms with the same base and adding their exponents.
Tips
A common mistake is to multiply the exponents instead of adding them when multiplying terms with the same base. For example, incorrectly calculating $x^3 \cdot x$ as $x^3$ or $x^9$ instead of $x^4$. Another common mistake is not recognizing that $x$ is the same as $x^1$.
AI-generated content may contain errors. Please verify critical information