Simplify the expression: $(x^2y^{-1})^2$
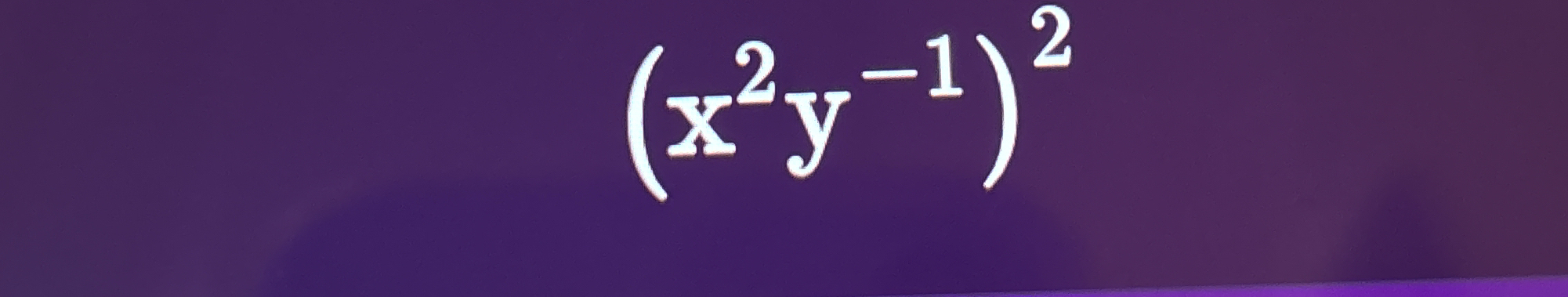
Understand the Problem
The question asks to simplify the given algebraic expression. We need to apply the power rule of exponents to simplify this expression.
Answer
$\frac{x^4}{y^2}$
Answer for screen readers
$\frac{x^4}{y^2}$
Steps to Solve
- Apply the power rule to $x^2$
The power rule states that $(a^m)^n = a^{m \cdot n}$. Applying this to $x^2$, we get:
$(x^2)^2 = x^{2 \cdot 2} = x^4$
- Apply the power rule to $y^{-1}$
Similarly, applying the power rule to $y^{-1}$, we get:
$(y^{-1})^2 = y^{-1 \cdot 2} = y^{-2}$
- Combine the results
Combining the simplified terms, we get:
$x^4y^{-2}$
- Rewrite with a positive exponent
To express the answer with positive exponents, we can rewrite $y^{-2}$ as $\frac{1}{y^2}$. Therefore, the simplified expression is:
$x^4y^{-2} = \frac{x^4}{y^2}$
$\frac{x^4}{y^2}$
More Information
The simplified form of the expression $(x^2y^{-1})^2$ with positive exponents is $\frac{x^4}{y^2}$. This is obtained using properties of exponents, specifically the power rule and the negative exponent rule.
Tips
A common mistake is forgetting to apply the outer exponent to both terms inside the parentheses. For example, some people might only apply the exponent to the $x^2$ term and not to the $y^{-1}$ term. Another mistake would be to miscalculate the exponents after applying the power rule, such as multiplying the exponents incorrectly.
AI-generated content may contain errors. Please verify critical information