Simplify the expression: $-\sqrt{\frac{7}{81}}$
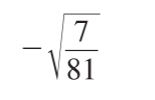
Understand the Problem
The question requires simplification of a mathematical expression involving a square root of a fraction. The numerator under the square root is 7, and the denominator is 81. The entire expression is negated. We need to simplify the square root and express the result as a simplified fraction.
Answer
$-\frac{\sqrt{7}}{9}$
Answer for screen readers
$-\frac{\sqrt{7}}{9}$
Steps to Solve
- Separate the square root
We can rewrite the expression by separating the square root of the numerator and the denominator:
$$-\sqrt{\frac{7}{81}} = -\frac{\sqrt{7}}{\sqrt{81}}$$
- Simplify the square root of the denominator
$\sqrt{81}$ simplifies to 9 because $9 \times 9 = 81$
$$-\frac{\sqrt{7}}{\sqrt{81}} = -\frac{\sqrt{7}}{9}$$
- Final Answer
Since 7 is a prime number, $\sqrt{7}$ cannot be simplified further. Thus, the simplified expression is $-\frac{\sqrt{7}}{9}$.
$-\frac{\sqrt{7}}{9}$
More Information
The number 7 is a prime number and 81 is a perfect square. A prime number cannot be simplified, but the square root of a perfect square is an integer.
Tips
A common mistake is to try to simplify $\sqrt{7}$ further, but since 7 is a prime number, it cannot be simplified. Another common mistake is forgetting the negative sign in front of the expression.
AI-generated content may contain errors. Please verify critical information