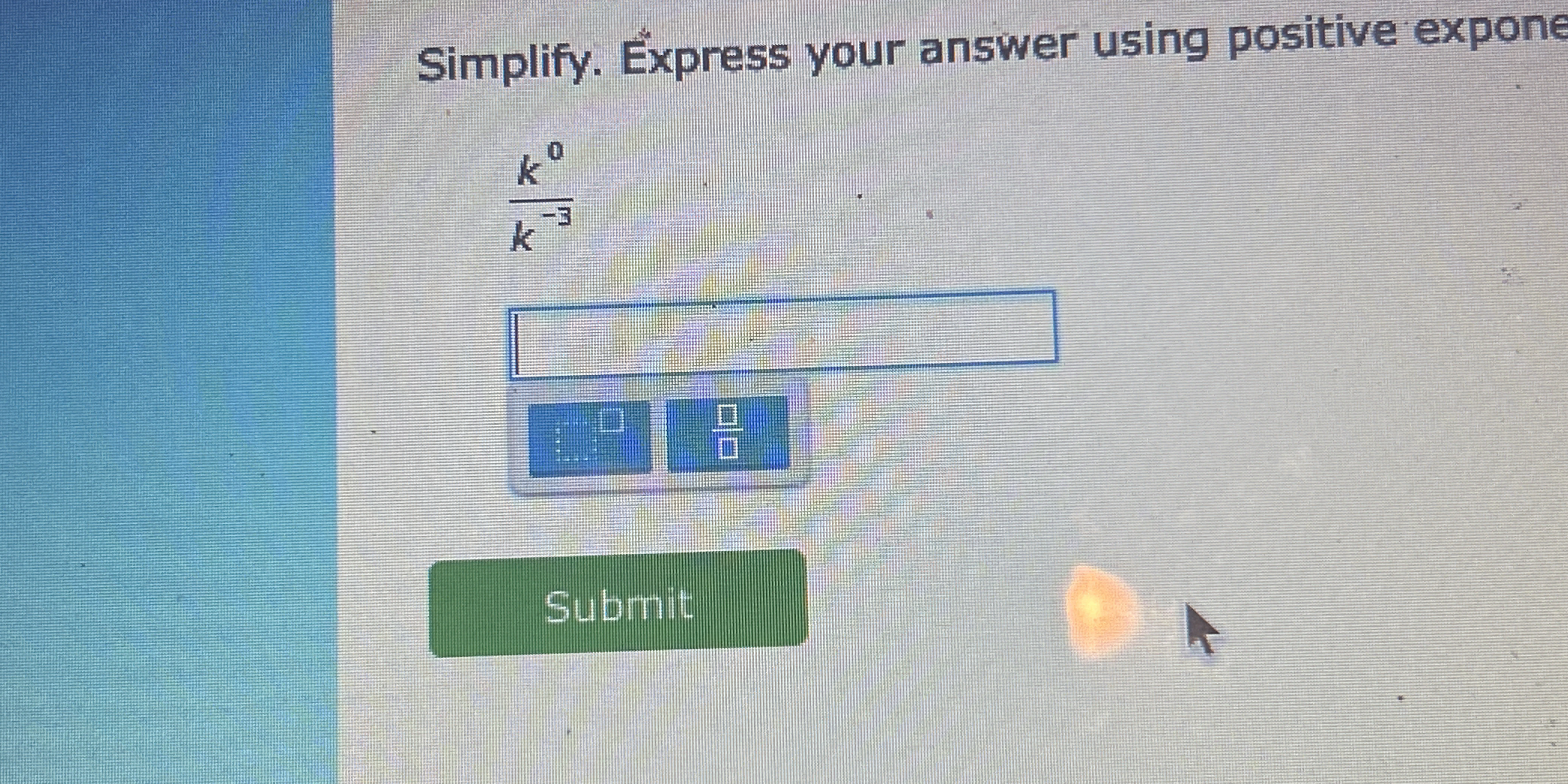
Simplify the expression k^0 / k^{-3}. Express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression ( \frac{k^0}{k^{-3}} ) and express the answer using positive exponents.
Answer
The simplified expression is \( k^3 \).
Answer for screen readers
The simplified expression is ( k^3 ).
Steps to Solve
-
Simplify the numerator
The numerator is ( k^0 ). According to the exponent rule, any non-zero base raised to the power of zero is equal to 1.
Thus, ( k^0 = 1 ). -
Rewrite the expression
Now substitute the numerator back into the expression:
$$ \frac{k^0}{k^{-3}} = \frac{1}{k^{-3}} $$ -
Apply the negative exponent rule
The negative exponent rule states that ( a^{-n} = \frac{1}{a^n} ). Hence, ( k^{-3} ) can be rewritten as:
$$ k^{-3} = \frac{1}{k^3} $$ -
Rewrite the fraction
Substituting this back into our expression gives us:
$$ \frac{1}{k^{-3}} = \frac{1}{\frac{1}{k^3}} $$ -
Simplify the entire expression
Now simplify the overall expression:
$$ \frac{1}{\frac{1}{k^3}} = k^3 $$
The simplified expression is ( k^3 ).
More Information
The simplification process utilized exponent rules extensively. Remember that ( k^0 = 1 ) and negative exponents switch the position of the base in a fraction.
Tips
- Forgetting that ( k^0 = 1 ) and not addressing the zero exponent correctly.
- Misapplying the negative exponent rule, leading to incorrect simplifications.
AI-generated content may contain errors. Please verify critical information