Simplify the expression: (5x - 3) + (2x + 8)
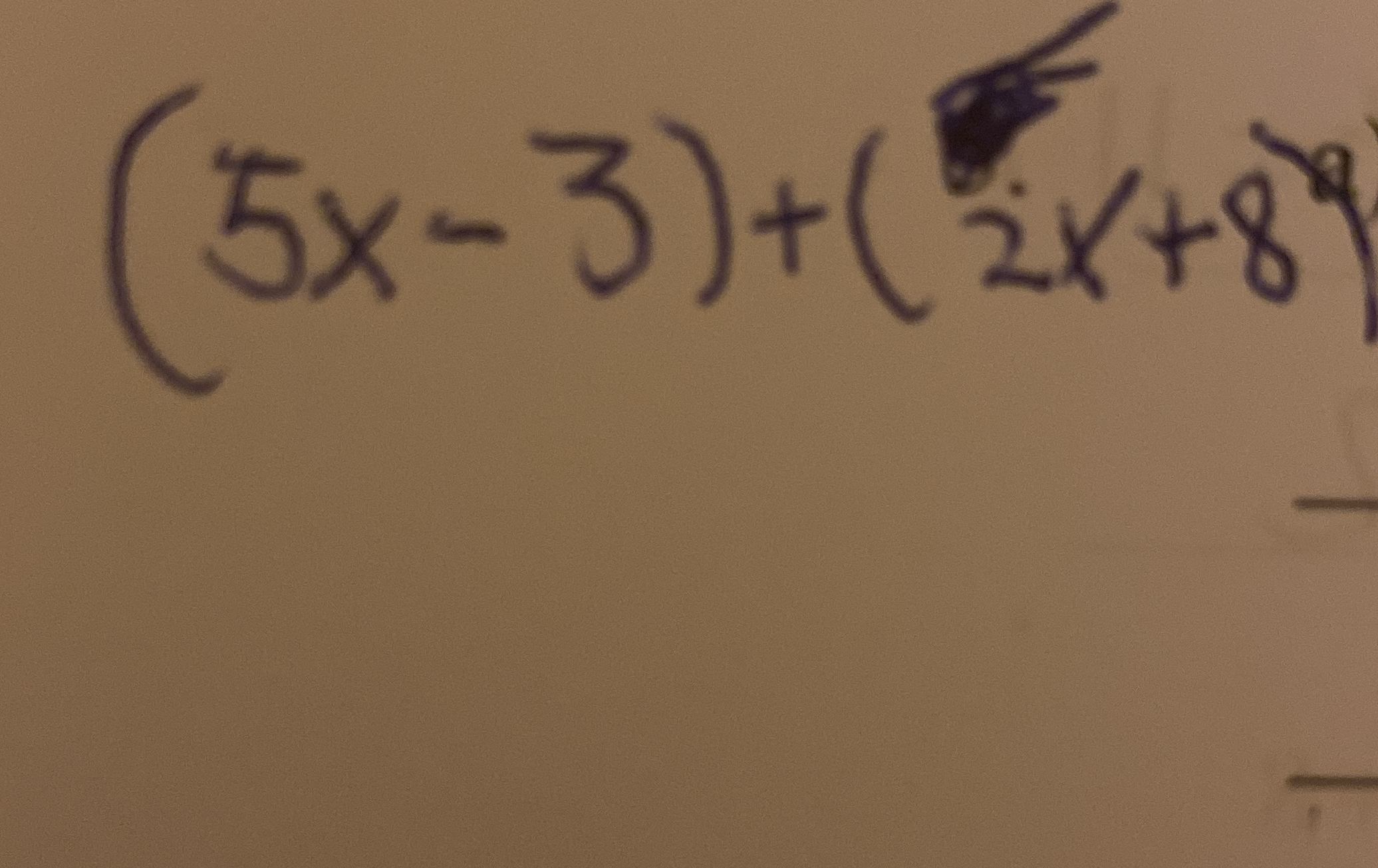
Understand the Problem
The question asks us to simplify the algebraic expression $(5x - 3) + (2x + 8)$. This involves combining like terms, which means adding the coefficients of the 'x' terms and adding the constant terms.
Answer
$7x + 5$
Answer for screen readers
$7x + 5$
Steps to Solve
-
Remove parentheses Since we are adding the two expressions, we can remove the parentheses without changing the signs. $$ (5x - 3) + (2x + 8) = 5x - 3 + 2x + 8$$
-
Group like terms Group the terms with 'x' and the constant terms together. $$ 5x + 2x - 3 + 8$$
-
Combine the 'x' terms Add the coefficients of the 'x' terms: $5x + 2x = (5+2)x = 7x$. $$ 7x - 3 + 8$$
-
Combine the constant terms Add the constant terms: $-3 + 8 = 5$. $$ 7x + 5$$
$7x + 5$
More Information
Combining like terms is a fundamental concept in algebra, used to simplify expressions and solve equations. The final expression, $7x+5$, represents the simplified form of the original expression.
Tips
A common mistake is to incorrectly combine unlike terms. For instance, adding $5x$ and a constant like $8$. Only terms with the same variable and exponent can be combined. Also, be careful with the signs of the numbers while adding or subtracting.
AI-generated content may contain errors. Please verify critical information