Simplify the expression: (5x - 3) + (15/2x + 8)
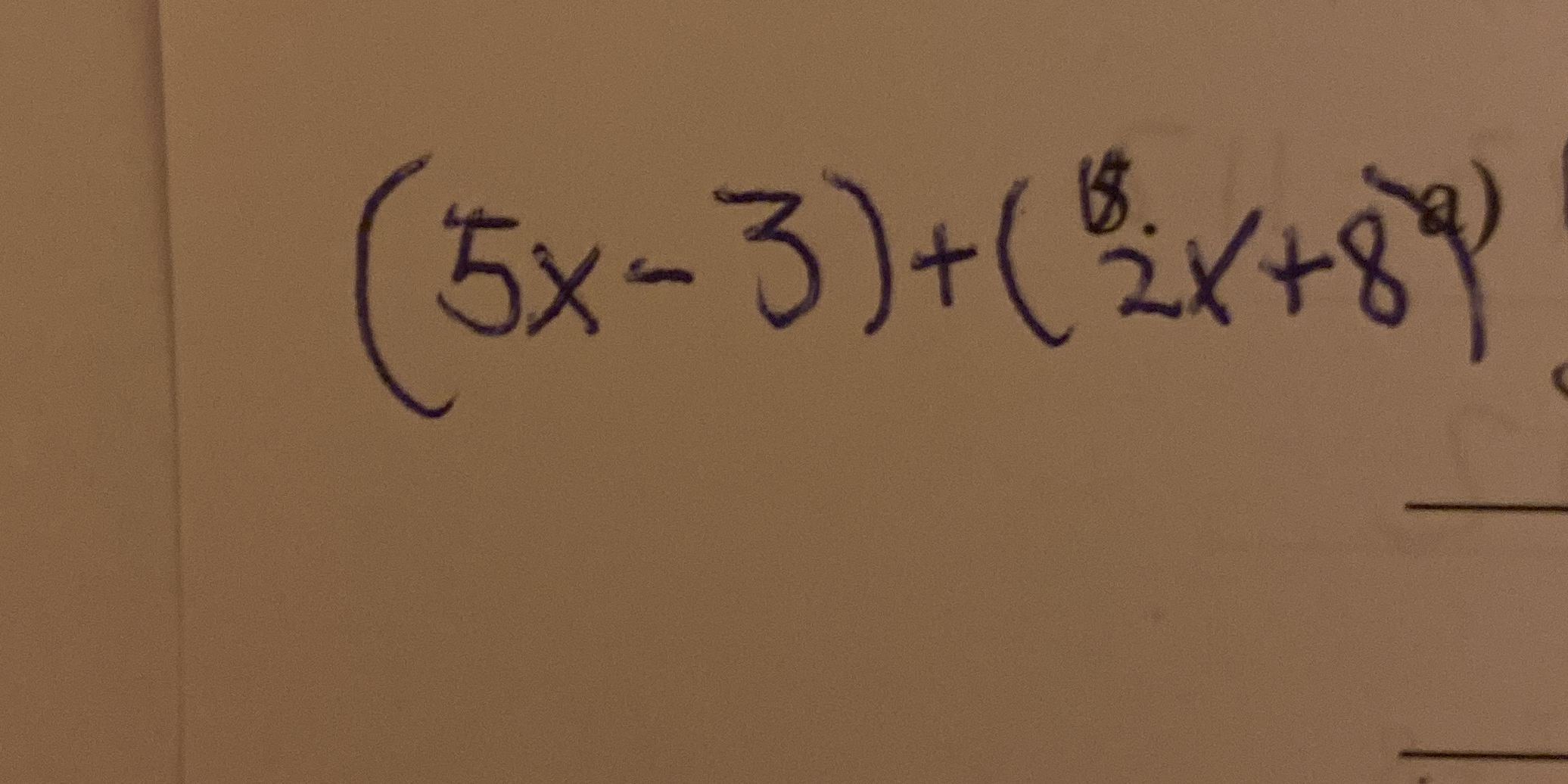
Understand the Problem
The question is asking us to simplify the algebraic expression by combining like terms. First, we need to remove the parentheses. Then, we can add the constants and x terms separately.
Answer
$\frac{25}{2}x + 5$
Answer for screen readers
$\frac{25}{2}x + 5$
Steps to Solve
- Remove parentheses
Since we are adding the two expressions, we can remove the parentheses without changing any signs.
$$(5x - 3) + (\frac{15}{2}x + 8) = 5x - 3 + \frac{15}{2}x + 8$$
- Combine x terms
Add the coefficients of the $x$ terms, $5$ and $\frac{15}{2}$. To do this, we need a common denominator, which is 2. So, we convert 5 to a fraction with a denominator of 2: $5 = \frac{10}{2}$.
$$5x + \frac{15}{2}x = \frac{10}{2}x + \frac{15}{2}x = \frac{10+15}{2}x = \frac{25}{2}x$$
- Combine constant terms
Add the constant terms, $-3$ and $8$.
$$-3 + 8 = 5$$
- Write the simplified expression
Combine the simplified x term and the simplified constant term.
$$\frac{25}{2}x + 5$$
$\frac{25}{2}x + 5$
More Information
The simplified expression is $\frac{25}{2}x + 5$. This is a linear expression in slope-intercept form, where the slope is $\frac{25}{2}$ and the y-intercept is $5$.
Tips
A common mistake is not finding a common denominator when adding the $x$ terms. Remember that you can only add fractions when they have the same denominator.
Another common mistake is incorrectly combining the constant terms, especially when one of them is negative.
AI-generated content may contain errors. Please verify critical information