Simplify the expression: (-5^8)^2
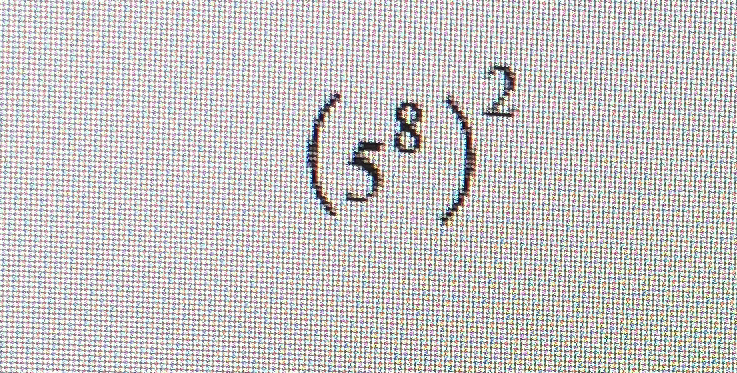
Understand the Problem
The question asks to simplify the expression (-5^8)^2. To simplify this expression, we need to apply the power of a power rule which states that (a^m)^n = a^(m*n). We also need to remember that a negative number raised to an even power will result in a positive number.
Answer
$5^{16}$
Answer for screen readers
$5^{16}$
Steps to Solve
- Apply the power of a power rule We have an expression of the form $(a^m)^n$. The power of a power rule states that we multiply the exponents: $(a^m)^n = a^{m \cdot n}$. In this case, we have $(-5^8)^2$.
Therefore, $(-5^8)^2 = (-1 \cdot 5^8)^2$
-
Distribute the exponent Apply the exponent outside the parenthesis to each term inside: $(-1 \cdot 5^8)^2 = (-1)^2 \cdot (5^8)^2$
-
Simplify the expression $(-1)^2 = 1$, also $(5^8)^2 = 5^{8*2} = 5^{16}$. Therefore, $(-1)^2 \cdot (5^8)^2 = 1 \cdot 5^{16} = 5^{16}$
$5^{16}$
More Information
$5^{16}$ is equal to 152,587,890,625.
Tips
A common mistake is to think that $(-5^8)$ is the same as $(-5)^8$. Remember that exponents only apply to what is directly to their left. Also, forgetting the rule $(a^m)^n = a^{m \cdot n}$ is a common mistake.
AI-generated content may contain errors. Please verify critical information