Simplify the expression: ((-3x)^2 (-5y)^3) / (25 (-x)^2 (-y))
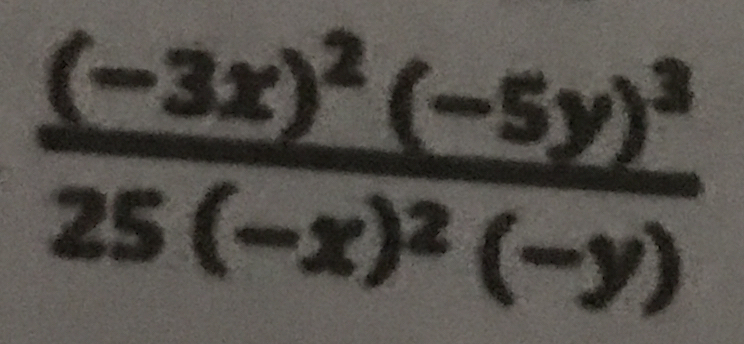
Understand the Problem
The question is asking to simplify the expression. We proceed by expanding the terms in the numerator and the denominator, and then cancelling out the common terms. Remember that a negative number squared is positive, but a negative number cubed is negative.
Answer
$45y^2$
Answer for screen readers
$45y^2$
Steps to Solve
-
Expand the numerator Expand $(-3x)^2$ and $(-5y)^3$. Remember that $(-3x)^2 = (-3)^2 \cdot x^2 = 9x^2$ and $(-5y)^3 = (-5)^3 \cdot y^3 = -125y^3$. Thus, the numerator becomes $9x^2 \cdot (-125y^3) = -1125x^2y^3$.
-
Expand the denominator Expand $(-x)^2$ and $(-y)$. $(-x)^2 = x^2$ and $(-y) = -y$. Thus, the denominator becomes $25 \cdot x^2 \cdot (-y) = -25x^2y$.
-
Simplify the expression Now we have $\frac{-1125x^2y^3}{-25x^2y}$. We can cancel out the common terms. $$ \frac{-1125x^2y^3}{-25x^2y} = \frac{-1125}{-25} \cdot \frac{x^2}{x^2} \cdot \frac{y^3}{y} $$ $$ \frac{-1125}{-25} = 45 $$ $$ \frac{x^2}{x^2} = 1$$ Note, $x \neq 0$ $$ \frac{y^3}{y} = y^2$$ Note, $y \neq 0$ Thus, the simplified expression is $45 \cdot 1 \cdot y^2 = 45y^2$.
$45y^2$
More Information
The simplified form of the given expression is $45y^2$, assuming that $x \neq 0$ and $y \neq 0$.
Tips
A common mistake is to forget to apply the exponent to the constant inside the parentheses, e.g., $(-3x)^2 = -9x^2$ instead of $9x^2$. Also, sign errors are common when dealing with negative numbers raised to powers. It's important to remember that a negative number raised to an even power is positive, while a negative number raised to an odd power is negative.
AI-generated content may contain errors. Please verify critical information