Simplify the expression: (-12k^6) / ((-k^4)^2(2k)^3)
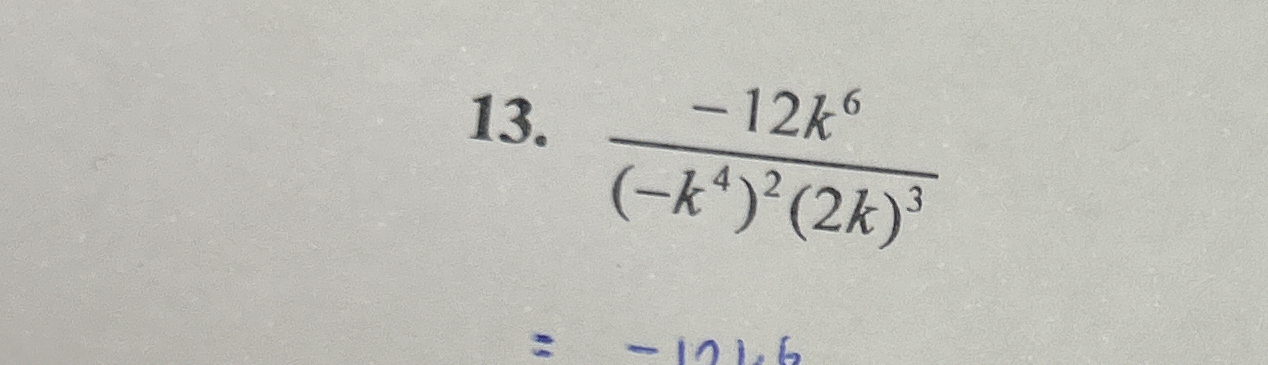
Understand the Problem
The question requires simplifying an algebraic expression involving exponents. We need to apply the rules of exponents to both the numerator and the denominator, and then reduce the expression to its simplest form.
Answer
$\frac{-3}{2k^5}$
Answer for screen readers
$\frac{-3}{2k^5}$
Steps to Solve
-
Simplify $(-k^4)^2$
When raising a power to a power, multiply the exponents. Also, note that a negative number squared becomes positive.
$(-k^4)^2 = (-1)^2 * (k^4)^2 = 1 * k^{4*2} = k^8$
-
Simplify $(2k)^3$
When raising a product to a power, raise each factor to the power.
$(2k)^3 = 2^3 * k^3 = 8k^3$
-
Rewrite the denominator
Replace $(-k^4)^2$ with $k^8$ and $(2k)^3$ with $8k^3$.
$k^8 * 8k^3 = 8k^{8+3} = 8k^{11}$
-
Rewrite the entire expression
Substitute the simplified denominator into the original expression.
$\frac{-12k^6}{8k^{11}}$
-
Simplify the fraction
Divide both the numerator and denominator by their greatest common factor.
$\frac{-12k^6}{8k^{11}} = \frac{-3k^6}{2k^{11}} = \frac{-3}{2} * \frac{k^6}{k^{11}}$
-
Simplify the exponents
When dividing terms with the same base, subtract the exponents.
$\frac{k^6}{k^{11}} = k^{6-11} = k^{-5} = \frac{1}{k^5}$
-
Final simplification
Rewrite with the simplified exponents.
$\frac{-3}{2} * \frac{1}{k^5} = \frac{-3}{2k^5}$
$\frac{-3}{2k^5}$
More Information
The expression is simplified by applying the power of a power rule, the power of a product rule, and the quotient of powers rule.
Tips
- Forgetting to apply the exponent to both the coefficient and the variable inside the parentheses. For example, $(2k)^3$ is $8k^3$, not $2k^3$.
- Incorrectly handling the negative sign when raising to a power. For example, $(-k^4)^2$ becomes positive because a negative number squared is positive.
- Making arithmetic errors when adding or subtracting exponents.
AI-generated content may contain errors. Please verify critical information