Simplify sin(60°) cos(15°) - sin(15°) cos(60°)
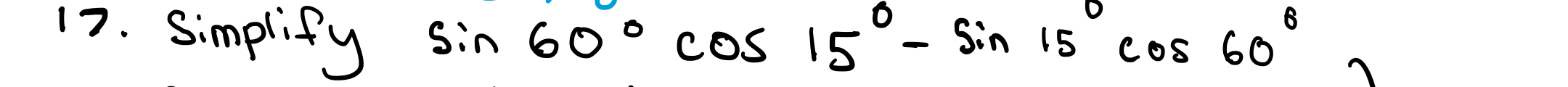
Understand the Problem
The question is asking to simplify the expression involving trigonometric functions: sin(60°) cos(15°) - sin(15°) cos(60°). We will apply trigonometric identities to find a simplified form.
Answer
The simplified expression is \( \frac{\sqrt{2}}{2} \).
Answer for screen readers
The simplified result is: $$ \frac{\sqrt{2}}{2} $$
Steps to Solve
-
Recognize the Identity We can apply the sine difference identity: $$ \sin(a) \cos(b) - \cos(a) \sin(b) = \sin(a - b) $$ By setting ( a = 60^\circ ) and ( b = 15^\circ ), the expression simplifies to: $$ \sin(60^\circ) \cos(15^\circ) - \sin(15^\circ) \cos(60^\circ) = \sin(60^\circ - 15^\circ) $$
-
Subtract the Angles Now compute the difference of the angles: $$ 60^\circ - 15^\circ = 45^\circ $$ Thus, we have: $$ \sin(60^\circ) \cos(15^\circ) - \sin(15^\circ) \cos(60^\circ) = \sin(45^\circ) $$
-
Evaluate ( \sin(45^\circ) ) The sine of ( 45^\circ ) is a well-known value: $$ \sin(45^\circ) = \frac{\sqrt{2}}{2} $$ Therefore, the final simplified expression is: $$ \sin(60^\circ) \cos(15^\circ) - \sin(15^\circ) \cos(60^\circ) = \frac{\sqrt{2}}{2} $$
The simplified result is: $$ \frac{\sqrt{2}}{2} $$
More Information
The value ( \frac{\sqrt{2}}{2} ) is significant in trigonometry, as it represents the sine (and cosine) of the angle ( 45^\circ ). This is often used in various applications from geometry to physics.
Tips
null
AI-generated content may contain errors. Please verify critical information