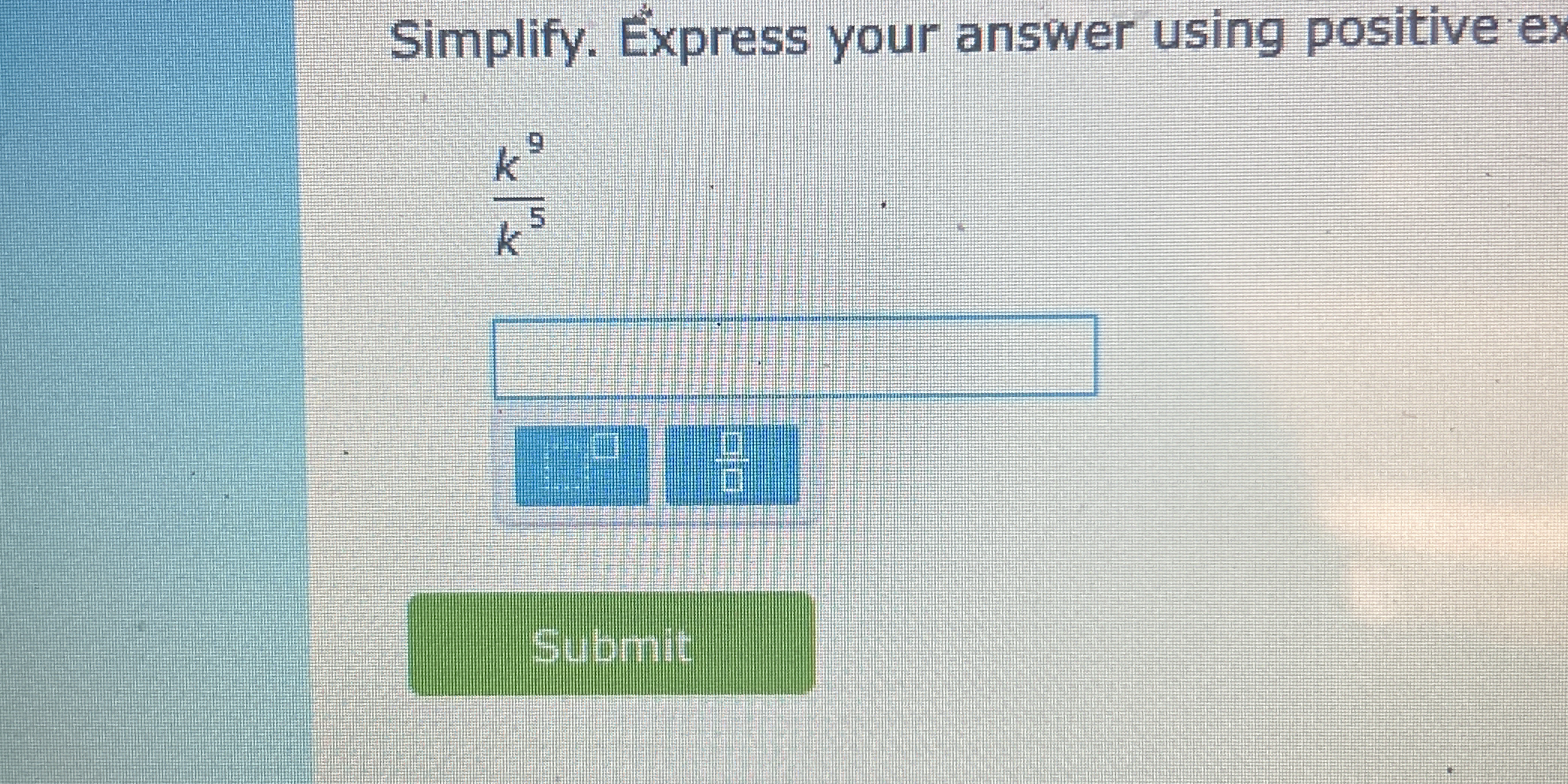
Simplify k^9 / k^5 and express your answer using positive exponents.
Understand the Problem
The question is asking us to simplify the expression k^9 / k^5 and to express the answer using positive exponents. This will involve applying the laws of exponents to simplify the fraction.
Answer
The simplified expression is $k^4$.
Answer for screen readers
The simplified expression is $k^4$.
Steps to Solve
-
Identify the Exponent Rule We will use the rule of exponents that states $\frac{a^m}{a^n} = a^{m-n}$ to simplify the expression.
-
Apply the Exponent Rule In our case, we have: $$ \frac{k^9}{k^5} = k^{9-5} $$
-
Calculate the Exponent Now, we compute the exponent: $$ 9 - 5 = 4 $$
Therefore, we have: $$ \frac{k^9}{k^5} = k^4 $$
- Ensure Positive Exponents Since the result $k^4$ already uses a positive exponent, we express our final answer as $k^4$.
The simplified expression is $k^4$.
More Information
Simplifying expressions using the laws of exponents is a fundamental algebraic skill. It allows us to reduce complex expressions into simpler forms, making calculations easier and clearer.
Tips
- Forgetting to subtract the exponents when simplifying.
- Confusing the exponent subtraction rule with multiplication. Always remember $\frac{a^m}{a^n} = a^{m-n}$.
AI-generated content may contain errors. Please verify critical information