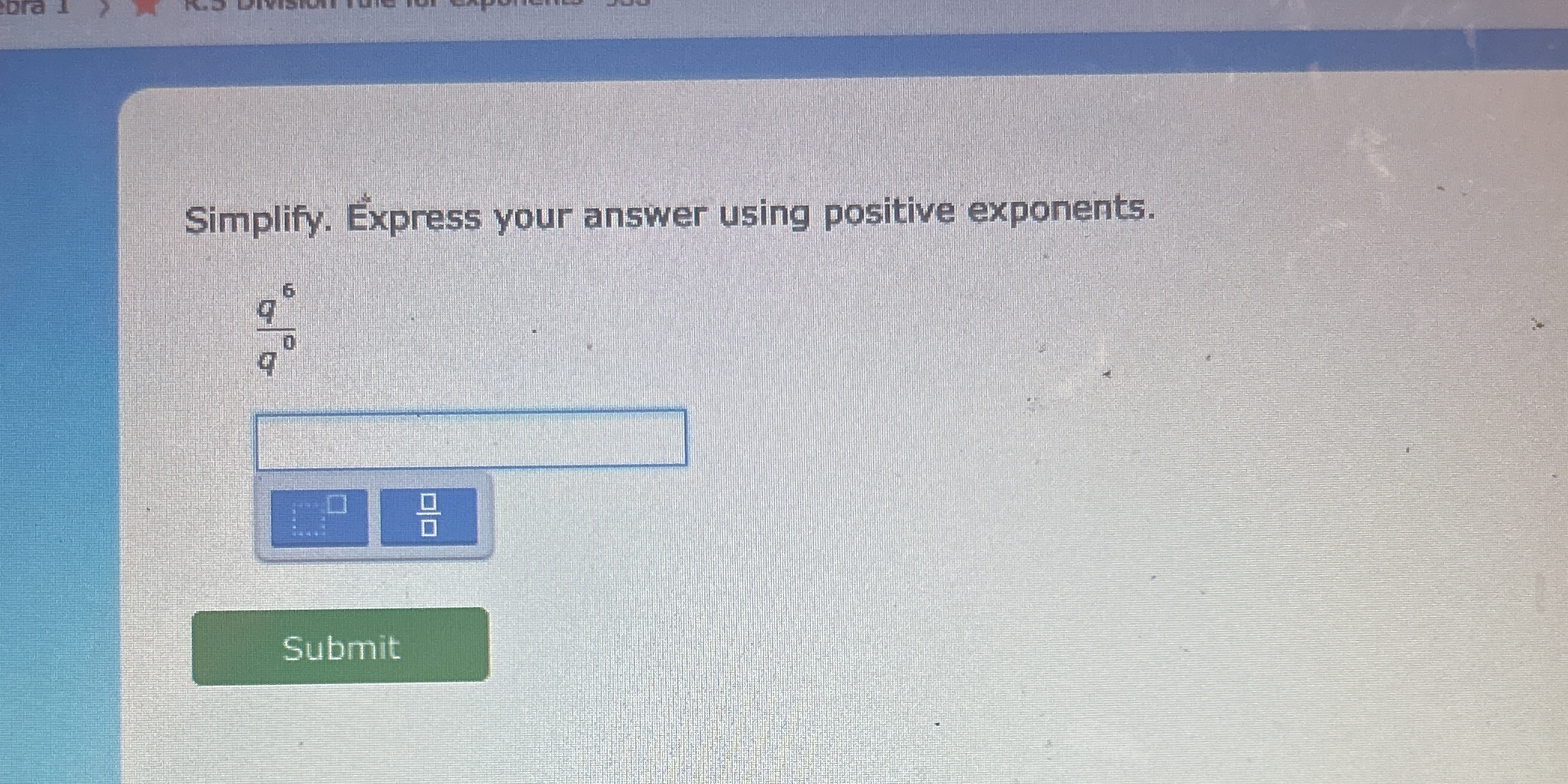
Simplify \( \frac{q^6}{q^0} \) and express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression ( \frac{q^6}{q^0} ) and to express the answer using positive exponents.
Answer
The simplified expression is \( q^6 \).
Answer for screen readers
The simplified expression is ( q^6 ).
Steps to Solve
- Identify the expression to simplify
We start with the expression ( \frac{q^6}{q^0} ).
- Use the property of exponents
Recall the division rule of exponents, which states that ( \frac{a^m}{a^n} = a^{m-n} ).
- Subtract the exponents
Apply the rule: $$ \frac{q^6}{q^0} = q^{6-0} = q^6 $$
- Express using positive exponents
Since ( q^6 ) is already expressed with a positive exponent, we conclude that:
The simplified form is ( q^6 ).
The simplified expression is ( q^6 ).
More Information
The exponent ( q^0 ) is equal to 1. Thus, dividing any number by 1 does not change its value, which is why we simplified it to ( q^6 ).
Tips
Some common mistakes include:
- Misapplying the exponent rules, such as thinking ( \frac{q^6}{q^0} ) equals 0 or 1 instead of applying the subtraction rule correctly.
- Forgetting that any non-zero number raised to the power of zero equals 1.
AI-generated content may contain errors. Please verify critical information