Simplify \(\frac{4x^2 - 16x}{x^2 - 16}\).
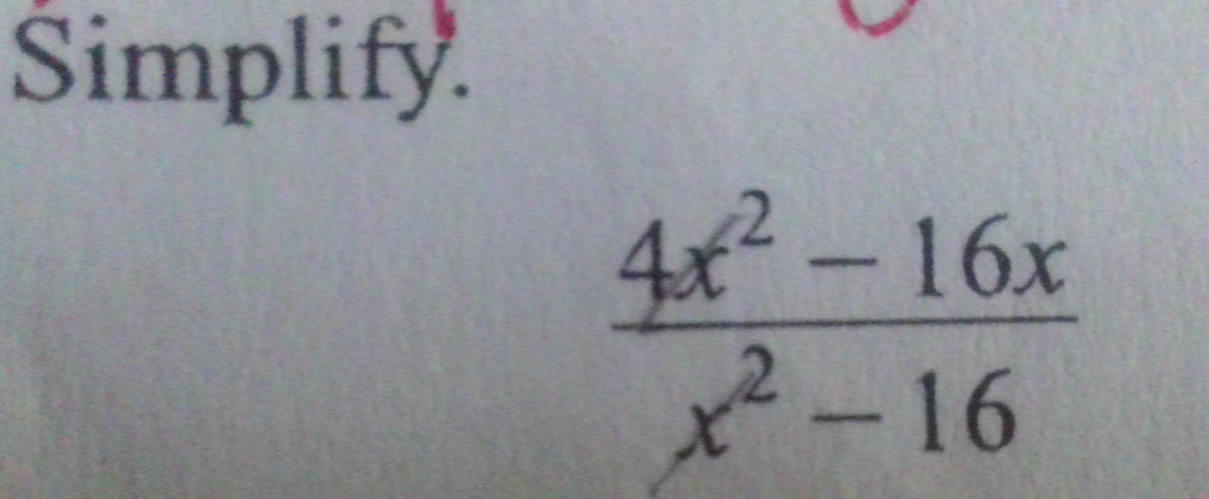
Understand the Problem
The question asks us to simplify the rational expression (\frac{4x^2 - 16x}{x^2 - 16}). To do this, we will factor both the numerator and the denominator and then cancel any common factors.
Answer
$\frac{4x}{x + 4}$
Answer for screen readers
$\frac{4x}{x + 4}$
Steps to Solve
- Factor the numerator
Factor out the greatest common factor, which is $4x$, from the numerator $4x^2 - 16x$: $$4x^2 - 16x = 4x(x - 4)$$
- Factor the denominator
Recognize that the denominator $x^2 - 16$ is a difference of squares: $$x^2 - 16 = (x - 4)(x + 4)$$
- Rewrite the rational expression
Substitute the factored forms of the numerator and the denominator into the original expression: $$\frac{4x^2 - 16x}{x^2 - 16} = \frac{4x(x - 4)}{(x - 4)(x + 4)}$$
- Cancel the common factors
Cancel the common factor of $(x - 4)$ from the numerator and the denominator: $$\frac{4x(x - 4)}{(x - 4)(x + 4)} = \frac{4x}{x + 4}$$
$\frac{4x}{x + 4}$
More Information
The original expression simplifies to $\frac{4x}{x + 4}$, where $x$ cannot be $4$ or $-4$, because that would make the denominator of the original expression equal to zero.
Tips
A common mistake is to try to cancel the $x$ terms in the final simplified expression $\frac{4x}{x+4}$. You cannot cancel the $x$ terms because the $x$ in the denominator is part of the sum $x+4$. You can only cancel factors, not terms. Another common mistake is not factoring completely.
AI-generated content may contain errors. Please verify critical information