Simplify $\frac{1}{(\frac{a-b}{a})(\frac{a-c}{a})}$
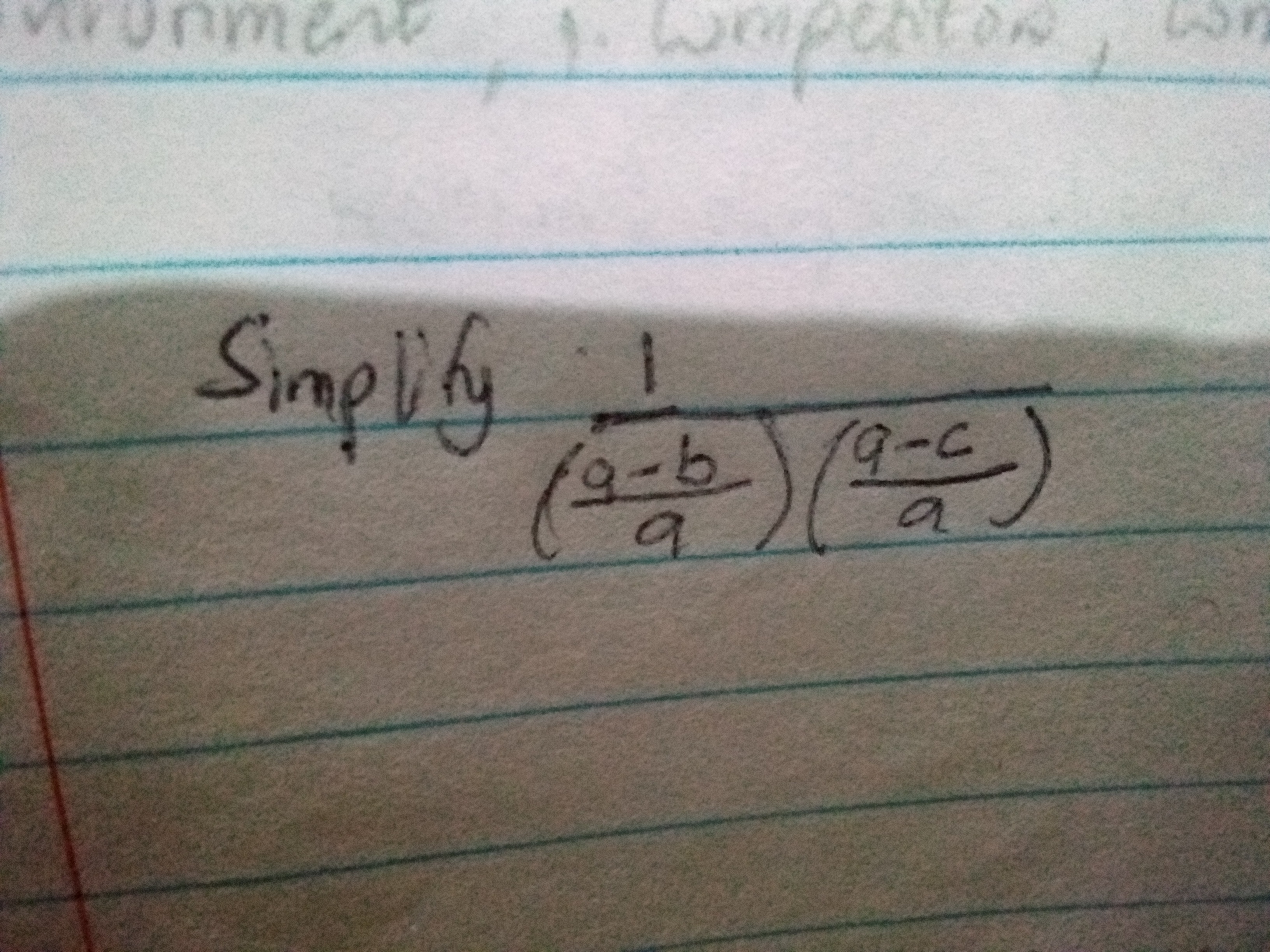
Understand the Problem
We need to simplify the given expression which involves fractions containing variables a, b, and c. The expression is a fraction where the numerator is 1, and the denominator is a product of two fractions, each having 'a' in the denominator.
Answer
$\frac{a^2}{(a-b)(a-c)}$
Answer for screen readers
$\frac{a^2}{(a-b)(a-c)}$
Steps to Solve
- Rewrite the expression
We start with the given expression:
$$ \frac{1}{(\frac{a-b}{a})(\frac{a-c}{a})} $$
- Multiply the terms in the denominator
Multiply the two fractions in the denominator together:
$$ \frac{a-b}{a} \cdot \frac{a-c}{a} = \frac{(a-b)(a-c)}{a^2} $$
- Substitute the result back into the original expression
Now the expression becomes:
$$ \frac{1}{\frac{(a-b)(a-c)}{a^2}} $$
- Simplify the complex fraction
Dividing by a fraction is the same as multiplying by its reciprocal. Therefore, we can rewrite the expression as:
$$ 1 \cdot \frac{a^2}{(a-b)(a-c)} = \frac{a^2}{(a-b)(a-c)} $$
$\frac{a^2}{(a-b)(a-c)}$
More Information
The simplified expression is $\frac{a^2}{(a-b)(a-c)}$. This represents the reciprocal of the product of the two original fractions in the denominator.
Tips
A common mistake is incorrectly multiplying or dividing fractions. Remember that when dividing by a fraction, you multiply by its reciprocal. Also, errors can occur during expansion of the product in the denominator, but in this case, expansion is not necessary for simplification, leaving the factors as $(a-b)(a-c)$.
AI-generated content may contain errors. Please verify critical information