Simplify. Express your answer using positive exponents: a^0 b^0 c^-1 · a b^-1 c^0 · a b · a b^-5 c^-6.

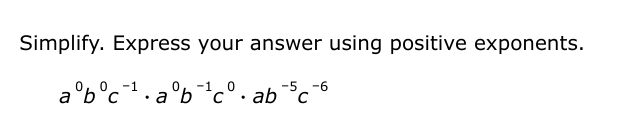
Understand the Problem

The question is asking to simplify the expression involving various variables raised to powers, emphasizing the need to express the final answer using only positive exponents.

Answer

$\frac{a^{3}}{b^{6} c^{7}}$

Steps to Solve

Identify the terms and their exponents

The expression is ( a^0 b^0 c^{-1} \cdot a b^{-1} c^{0} \cdot ab \cdot a b^{-5} c^{-6} ).

Apply the property of exponents that states (x^0 = 1)

Both (a^0) and (b^0) equal 1, so we can simplify:

$$ a^0 b^0 = 1 $$

Thus, the expression simplifies to:

$$ 1 \cdot c^{-1} \cdot a b^{-1} \cdot ab \cdot a b^{-5} c^{-6} $$

Multiply the remaining terms and combine like bases

Combine similar bases together while adding their exponents:

For (a): $$ a^{1+1+1} = a^{3} $$
For (b): $$ b^{-1-5} = b^{-6} $$
For (c): $$ c^{-1-6} = c^{-7} $$

Putting this together gives:

$$ a^{3} b^{-6} c^{-7} $$

Express using only positive exponents

To ensure all exponents are positive, we rewrite the expression:

$$ \frac{a^{3}}{b^{6} c^{7}} $$

The simplified expression is (\frac{a^{3}}{b^{6} c^{7}}).

More Information

When simplifying expressions with exponents, it's crucial to remember the properties of exponents that allow for the combination and simplification of terms. This expression also highlights understanding how to convert negative exponents into a fraction form with positive exponents.

Tips

Forgetting that (x^0 = 1) and keeping (a^0) or (b^0) in the expression.
Miscalculating the exponents when combining like bases (e.g., adding instead of subtracting).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!