Simplify: $6\sqrt{5t^3} \cdot \sqrt{15t^5}$
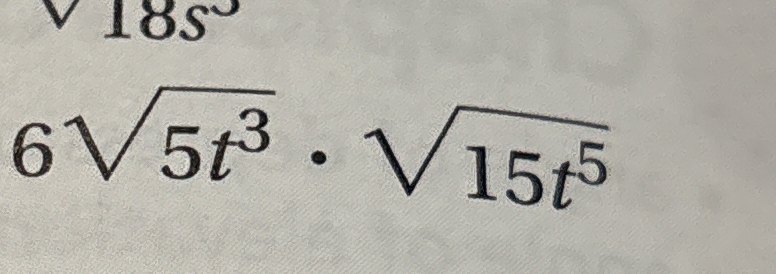
Understand the Problem
The problem asks us to simplify an expression involving radicals. We will need to use the properties of radicals to combine and simplify the expression, extracting any perfect square factors from under the square roots.
Answer
$30t^4\sqrt{3}$
Answer for screen readers
$30t^4\sqrt{3}$
Steps to Solve
-
Combine the radicals We can combine the two radicals into a single radical by using the property $\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$. $$6\sqrt{5t^3} \cdot \sqrt{15t^5} = 6\sqrt{(5t^3)(15t^5)}$$
-
Simplify the expression inside the radical Multiply the terms inside the radical. Remember that $t^3 \cdot t^5 = t^{3+5} = t^8$. Also, $5 \cdot 15 = 75$. $$6\sqrt{75t^8}$$
-
Factor out perfect squares We can factor $75$ as $25 \cdot 3$, where $25 = 5^2$ is a perfect square. Also, $t^8 = (t^4)^2$ is a perfect square. $$6\sqrt{25 \cdot 3 \cdot t^8}$$
-
Extract the perfect squares from the radical We can extract the square roots of the perfect squares: $\sqrt{25} = 5$ and $\sqrt{t^8} = t^4$. $$6 \cdot 5 \cdot t^4 \sqrt{3}$$
-
Simplify the expression Multiply the constants together: $6 \cdot 5 = 30$. $$30t^4\sqrt{3}$$
$30t^4\sqrt{3}$
More Information
The simplified form of the given expression is $30t^4\sqrt{3}$.
Tips
A common mistake is forgetting to simplify the radical completely. For example, someone might stop at $6\sqrt{75t^8}$ without factoring out the perfect squares. Another common mistake is incorrectly multiplying or simplifying the exponents.
AI-generated content may contain errors. Please verify critical information