Simplify (5x - 3) + (15/2 x + 8).
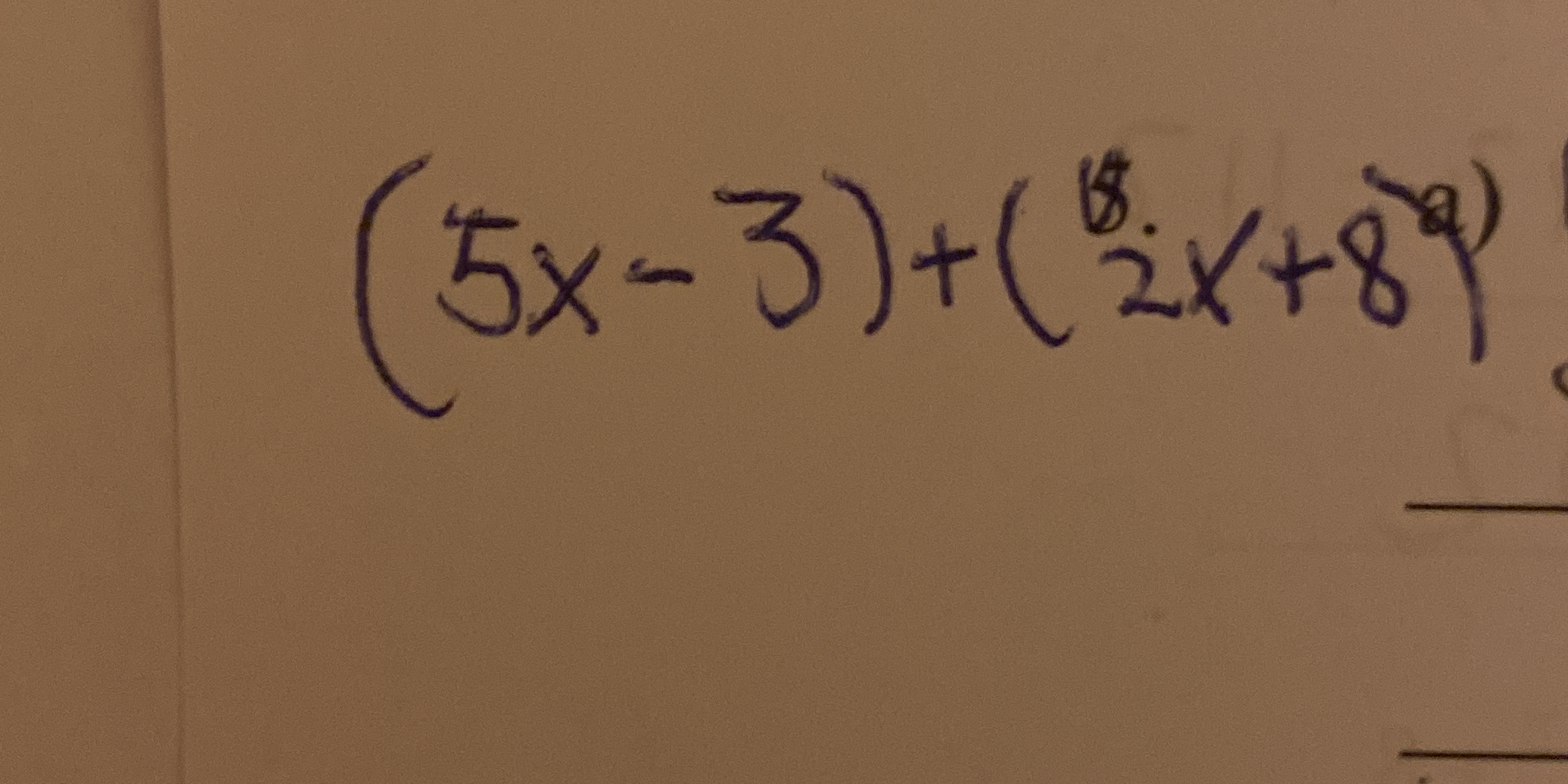
Understand the Problem
The user is asking to simplify the expression (5x - 3) + (15/2 x + 8). We will remove the parenthesis and combine like terms.
Answer
$\frac{25}{2}x + 5$
Answer for screen readers
$\frac{25}{2}x + 5$
Steps to Solve
-
Remove parentheses Since we are adding the two terms together, we can remove the parentheses without changing the expression: $5x - 3 + \frac{15}{2}x + 8$
-
Group like terms Group the terms containing $x$ and the constant terms together: $(5x + \frac{15}{2}x) + (-3 + 8)$
-
Combine the x terms To add $5x$ and $\frac{15}{2}x$, we need a common denominator. Convert $5x$ to $\frac{10}{2}x$: $\frac{10}{2}x + \frac{15}{2}x = \frac{25}{2}x$
-
Combine the Constants Add the constant terms $-3$ and $8$: $-3 + 8 = 5$
-
Write the simplified expression Combine the simplified x terms and the constant term: $\frac{25}{2}x + 5$
$\frac{25}{2}x + 5$
More Information
The expression $(5x - 3) + (\frac{15}{2}x + 8)$ simplifies to $\frac{25}{2}x + 5$.
Tips
A common mistake is not finding the common denominator when adding the x terms. Also, mistakes can be made when adding negative and positive numbers.
AI-generated content may contain errors. Please verify critical information