Simplify $3\sqrt{7} - \sqrt{63}$
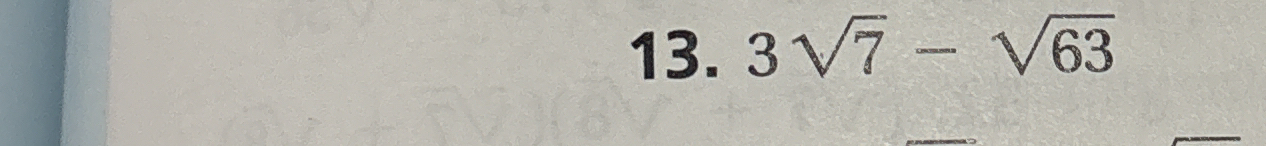
Understand the Problem
The question asks to simplify the expression $3\sqrt{7} - \sqrt{63}$. This involves simplifying the square root term and then combining like terms.
Answer
0
Answer for screen readers
0
Steps to Solve
- Simplify $\sqrt{63}$
To simplify $\sqrt{63}$, find its prime factorization. $63 = 9 \times 7 = 3^2 \times 7$. Therefore, $\sqrt{63} = \sqrt{3^2 \times 7} = \sqrt{3^2} \times \sqrt{7} = 3\sqrt{7}$.
- Substitute simplified form back into the original expression
Replace $\sqrt{63}$ with $3\sqrt{7}$ in the original expression:
$3\sqrt{7} - \sqrt{63} = 3\sqrt{7} - 3\sqrt{7}$
- Combine like terms
Since both terms now have the same radical part, $\sqrt{7}$, we can combine them:
$3\sqrt{7} - 3\sqrt{7} = (3 - 3)\sqrt{7} = 0\sqrt{7} = 0$
0
More Information
The simplified expression equals 0.
Tips
A common mistake is not simplifying $\sqrt{63}$ correctly or forgetting to combine the terms after simplification.
AI-generated content may contain errors. Please verify critical information