Simplify (3^5)^6
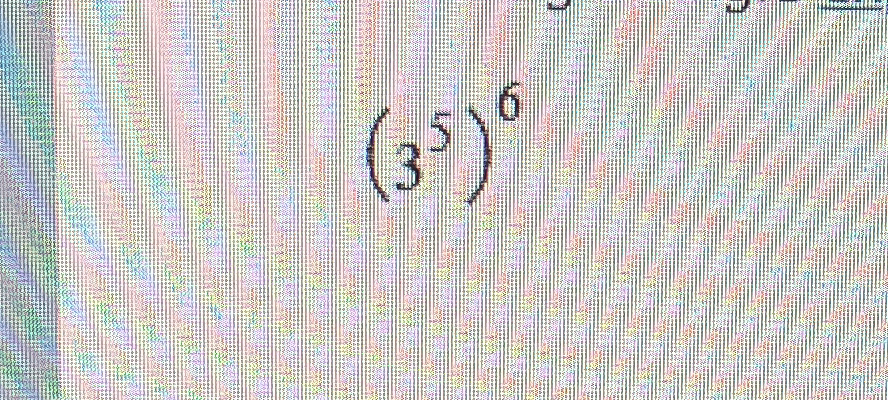
Understand the Problem
The question is asking us to simplify an expression with exponents. We will use the power of a power rule to rewrite the expression with a single exponent.
Answer
$3^{30}$
Answer for screen readers
$3^{30}$
Steps to Solve
- Identify the power of a power rule
The power of a power rule states that $(a^m)^n = a^{m \cdot n}$.
- Apply the power of a power rule
In the given expression $(3^5)^6$, we have $a = 3$, $m = 5$, and $n = 6$. Therefore, we can rewrite the expression as:
$(3^5)^6 = 3^{5 \cdot 6}$
- Simplify the exponent
Multiply the exponents:
$5 \cdot 6 = 30$
So, the expression becomes:
$3^{30}$
$3^{30}$
More Information
The expression $(3^5)^6$ simplifies to $3^{30}$. This is a very large number: 205,891,132,094,649.
Tips
A common mistake is to add the exponents instead of multiplying them. Remember that $(a^m)^n = a^{m \cdot n}$, not $a^{m+n}$.
AI-generated content may contain errors. Please verify critical information