Simplify (2a^3)^4(a^3)^3
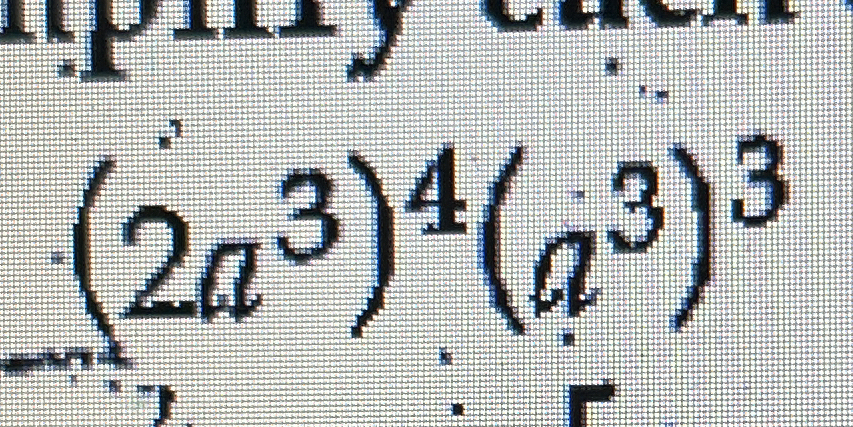
Understand the Problem
The question is asking to simplify the expression given, which involves powers of numbers and variables. We'll apply the laws of exponents to combine like terms effectively.
Answer
$16a^{21}$
Answer for screen readers
The simplified expression is $16a^{21}$.
Steps to Solve
- Apply the Power of a Product Rule
Start by applying the power of a product rule, which states that $(xy)^n = x^n y^n$. For the first term $(2a^{3})^{4}$:
$$ (2a^{3})^{4} = 2^{4} \cdot (a^{3})^{4} $$
- Calculate the Individual Powers
Now compute the powers:
-
Calculate $2^{4}$: $$ 2^{4} = 16 $$
-
For $(a^{3})^{4}$, use the power of a power rule: $$ (a^{3})^{4} = a^{3 \cdot 4} = a^{12} $$
So, the first term simplifies to: $$ (2a^{3})^{4} = 16a^{12} $$
- Simplify the Second Term
Now simplify the second term $(a^{3})^{3}$:
Using the power of a power rule: $$ (a^{3})^{3} = a^{3 \cdot 3} = a^{9} $$
- Combine the Results
Now combine the simplified terms:
$$ 16a^{12} \cdot a^{9} $$
- Use the Laws of Exponents to Combine Like Terms
Add the exponents of the like bases: $$ a^{12} \cdot a^{9} = a^{12 + 9} = a^{21} $$
So, the final expression is: $$ 16a^{21} $$
The simplified expression is $16a^{21}$.
More Information
The laws of exponents make it easier to simplify expressions involving powers. In this case, we used three important laws: the power of a product, the power of a power, and the law of exponents for multiplying like bases.
Tips
- Forgetting to apply the power of a product rule correctly, which can lead to incorrect individual term simplifications.
- Adding exponents incorrectly when combining like bases.
AI-generated content may contain errors. Please verify critical information