Simplify (2a^3)^4 * (a^3)^3.
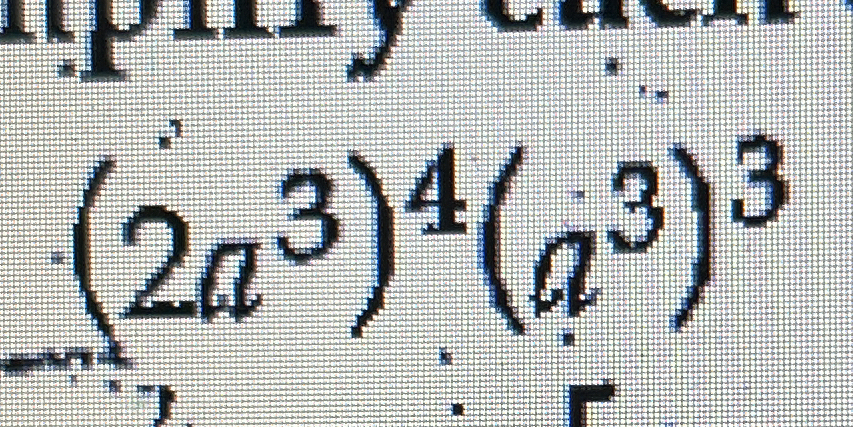
Understand the Problem
The question is asking how to simplify the expression (2a^3)^4 * (a^3)^3. This involves applying the rules of exponents to combine the terms and simplify the expression.
Answer
The simplified expression is \( 16a^{21} \).
Answer for screen readers
The simplified expression is ( 16a^{21} ).
Steps to Solve
- Apply the power rule to each term
Using the power rule of exponents, $(x^m)^n = x^{mn}$, we first simplify each part of the expression:
-
For $(2a^3)^4$: $$ (2a^3)^4 = 2^4 \cdot (a^3)^4 = 16 \cdot a^{12} $$
-
For $(a^3)^3$: $$ (a^3)^3 = a^{3 \cdot 3} = a^9 $$
- Combine the results
Now, we can combine the simplified terms: $$ (2a^3)^4 \cdot (a^3)^3 = (16a^{12}) \cdot (a^9) $$
- Add the exponents of like terms
Since the bases are the same (both are $a$), we can add the exponents: $$ a^{12 + 9} = a^{21} $$
- Write the final expression
Thus, combining everything gives us: $$ 16a^{21} $$
The simplified expression is ( 16a^{21} ).
More Information
This expression demonstrates the use of the power rule and the properties of exponents, showing how to handle both numerical and variable components together.
Tips
- Forgetting to apply the power rule correctly, especially when raising a product to a power.
- Not adding the exponents correctly when combining like terms.
AI-generated content may contain errors. Please verify critical information