Simplify -2√(7x²) * (1/3)√(28x³)
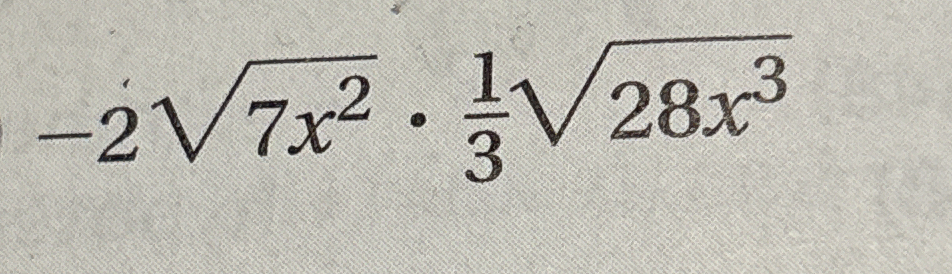
Understand the Problem
The question asks to simplify the expression shown in the image. This involves simplifying radicals and combining like terms. We will simplify each radical term independently and then combine them.
Answer
$ -\frac{28x^2\sqrt{x}}{3} $
Answer for screen readers
$ -\frac{28x^2\sqrt{x}}{3} $
Steps to Solve
- Simplify the first radical
We simplify $-2\sqrt{7x^2}$. Assuming $x$ is non-negative, $\sqrt{x^2} = x$. Therefore, $-2\sqrt{7x^2} = -2x\sqrt{7}$.
- Simplify the second radical
We simplify $\frac{1}{3}\sqrt{28x^3}$. First, we can factor 28 as $4 \cdot 7$ and $x^3$ as $x^2 \cdot x$. Then $$ \frac{1}{3} \sqrt{28x^3} = \frac{1}{3} \sqrt{4 \cdot 7 \cdot x^2 \cdot x} $$ $$ = \frac{1}{3} \sqrt{4x^2 \cdot 7x} = \frac{1}{3} (2x) \sqrt{7x} = \frac{2x}{3} \sqrt{7x} $$
- Multiply the simplified radicals
Multiply the results from step 1 and step 2: $$ (-2x\sqrt{7}) \cdot (\frac{2x}{3} \sqrt{7x}) $$ $$ = \frac{-4x^2}{3} \sqrt{7 \cdot 7 \cdot x} $$ $$ = \frac{-4x^2}{3} \sqrt{49x} = \frac{-4x^2}{3} (7\sqrt{x}) = \frac{-28x^2\sqrt{x}}{3} $$
$ -\frac{28x^2\sqrt{x}}{3} $
More Information
The simplified form of the expression is $ -\frac{28x^2\sqrt{x}}{3} $. This assumes that x is non-negative.
Tips
A common mistake is not simplifying the radicals completely before multiplying. Another mistake is incorrectly multiplying the coefficients and the terms inside the square roots. For example, some might forget to take the square root of $x^2$ as $x$ or incorrectly simplify $\sqrt{28}$ to $2\sqrt{14}$ instead of $2\sqrt{7}$. Also, forgetting to multiply the coefficients outside the square root. Lastly, a mistake might be made when forgetting to combine the terms under the radicals correctly, e.g., $\sqrt{7} * \sqrt{7x} = \sqrt{49x}$.
AI-generated content may contain errors. Please verify critical information