Simplify: 1/x + 3/x^3
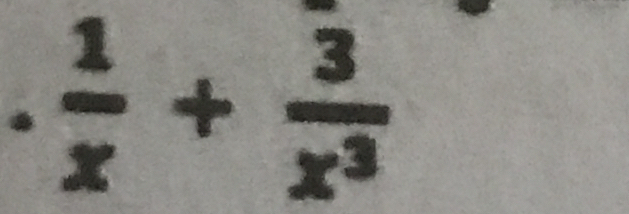
Understand the Problem
The question requires to add two fractions with polynomial denominators. We need to find a common denominator to perform the addition.
Answer
$\frac{x^2 + 3}{x^3}$
Answer for screen readers
$\frac{x^2 + 3}{x^3}$
Steps to Solve
- Find the least common denominator (LCD)
The denominators are $x$ and $x^3$. The LCD is $x^3$.
- Rewrite the fractions with the LCD
Rewrite $\frac{1}{x}$ with the denominator $x^3$. To do this, multiply the numerator and denominator by $x^2$: $$ \frac{1}{x} = \frac{1 \cdot x^2}{x \cdot x^2} = \frac{x^2}{x^3} $$ The second fraction, $\frac{3}{x^3}$, already has the LCD as its denominator.
- Add the fractions
Add the rewritten fractions: $$ \frac{x^2}{x^3} + \frac{3}{x^3} = \frac{x^2 + 3}{x^3} $$
$\frac{x^2 + 3}{x^3}$
More Information
When adding fractions, a common denominator is required. The least common denominator simplifies calculations.
Tips
A common mistake is to add the numerators and denominators separately, which is incorrect. Another mistake is not finding the least common denominator and instead multiplying the existing denominators which will result in more complex simplification in later steps.
AI-generated content may contain errors. Please verify critical information