Simplify 12-(3x-2)-(5x+4)
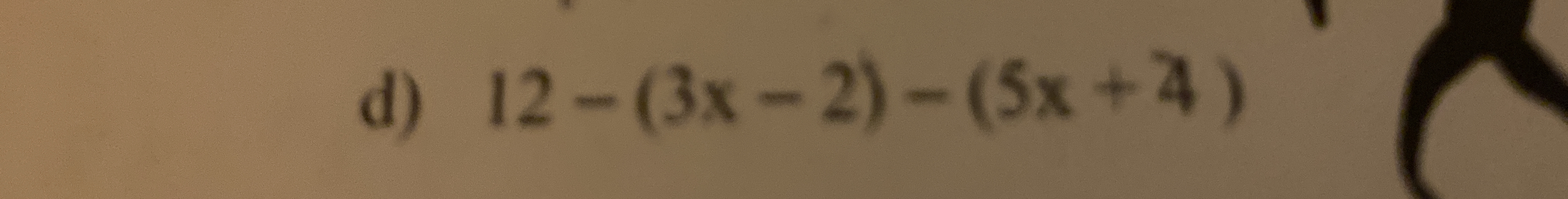
Understand the Problem
The question asks to simplify the expression by distributing the negative signs and then combining like terms. The expression involves arithmetic and algebraic manipulation.
Answer
$10 - 8x$
Answer for screen readers
$10 - 8x$
Steps to Solve
- Distribute the first negative sign
Distribute the negative sign in front of the first parenthesis $(3x - 2)$
$12 - (3x - 2) = 12 - 3x + 2$
- Distribute the second negative sign
Distribute the negative sign in front of the second parenthesis $(5x + 4)$
$12 - 3x + 2 - (5x + 4) = 12 - 3x + 2 - 5x - 4$
- Combine like terms
Combine the $x$ terms and the constant terms
$12 + 2 - 4 - 3x - 5x = (12 + 2 - 4) + (-3x - 5x)$
- Simplify
Simplify the expression to get the final answer
$10 - 8x$
$10 - 8x$
More Information
The simplified expression is $10-8x$.
Tips
A common mistake is not distributing the negative sign correctly to all terms inside the parentheses. For instance, forgetting to change the sign of the $-2$ in the first parentheses, or the $4$ in the second parentheses will lead to an incorrect answer. Another common mistake is incorrectly combining like terms.
AI-generated content may contain errors. Please verify critical information