Simplify: (1-h^2) / (2h^2 - 10h - 12) ÷ (2h-2) / 6
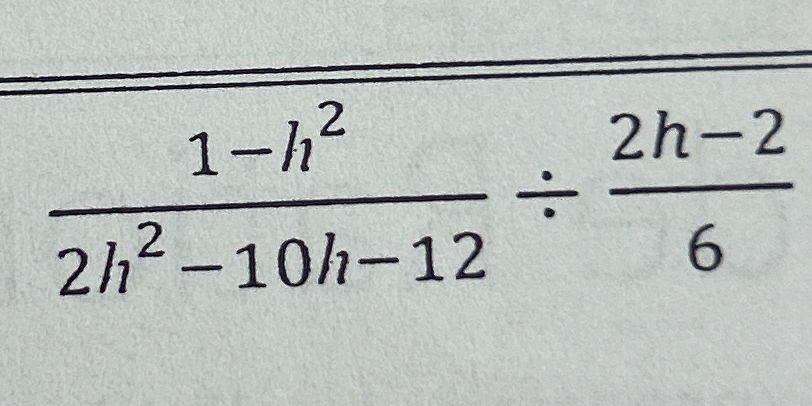
Understand the Problem
The question is asking us to simplify a fraction division problem. This involves factoring, inverting the second fraction and multiplying, and then simplifying the resulting expression.
Answer
$\frac{-3}{2h-12}$
Answer for screen readers
$\frac{-3}{2h-12}$
Steps to Solve
-
Rewrite division as multiplication Dividing by a fraction is the same as multiplying by its reciprocal. So, we have: $$ \frac{1-h^2}{2h^2-10h-12} \div \frac{2h-2}{6} = \frac{1-h^2}{2h^2-10h-12} \cdot \frac{6}{2h-2} $$
-
Factor the expressions Now, factor each of the polynomials: $1 - h^2 = (1-h)(1+h)$ $2h^2 - 10h - 12 = 2(h^2 - 5h - 6) = 2(h-6)(h+1)$ $2h - 2 = 2(h-1)$
-
Rewrite the expression with factored forms Substitute the factored forms into the expression: $$ \frac{(1-h)(1+h)}{2(h-6)(h+1)} \cdot \frac{6}{2(h-1)} $$
-
Simplify the expression Cancel out common factors and simplify: $$ \frac{(1-h)(1+h)}{2(h-6)(h+1)} \cdot \frac{6}{2(h-1)} = \frac{-(h-1)(h+1)}{2(h-6)(h+1)} \cdot \frac{6}{2(h-1)} $$ $$ = \frac{-(h-1)}{2(h-6)} \cdot \frac{6}{2(h-1)} = \frac{-1}{2(h-6)} \cdot \frac{6}{2} $$ $$ = \frac{-1}{2(h-6)} \cdot 3 = \frac{-3}{2(h-6)} $$
-
Final simplified form $$ \frac{-3}{2(h-6)} = \frac{-3}{2h-12} $$
$\frac{-3}{2h-12}$
More Information
The simplified form of the given expression is $\frac{-3}{2h-12}$.
Tips
A common mistake is not factoring out the expressions correctly or missing some factors during simplification. Another mistake could be not realizing that $(1-h) = -(h-1)$. Also not distributing properly in the last step.
AI-generated content may contain errors. Please verify critical information