Si una conductora se desplazará desde el punto C al punto A, ¿cuál es la distancia d que recorrerá la conductora?
Understand the Problem
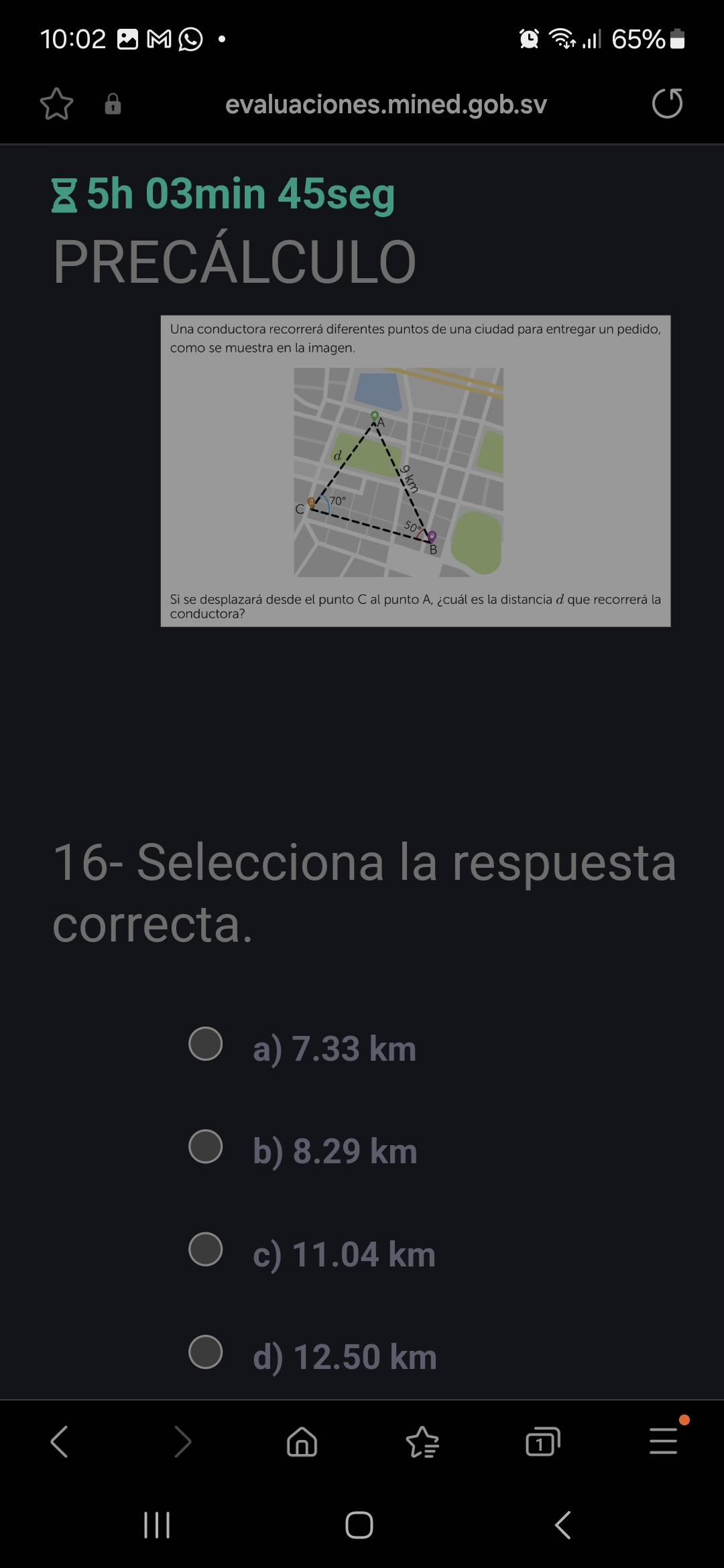
El problema describe la ruta de una conductora que entrega un pedido y recorre diferentes puntos en una ciudad. Se presenta un diagrama con un triángulo representado en un mapa, donde se conocen las distancias y los ángulos. El problema pregunta específicamente, la distancia desde el punto C al punto A, representada por la variable 'd'.
Answer
$7.33$ km
Answer for screen readers
a) $7.33$ km
Steps to Solve
-
Hallar el ángulo en el punto A Dado que la suma de los ángulos en un triángulo es 180 grados, podemos encontrar el ángulo en el punto A: $A = 180^\circ - B - C = 180^\circ - 50^\circ - 70^\circ = 60^\circ$
-
Usar la Ley de los Senos para hallar la distancia 'd' La Ley de los Senos establece que la razón entre la longitud de un lado de un triángulo y el seno del ángulo opuesto es constante para todos los lados y ángulos en ese triángulo. Podemos usarla para encontrar la distancia $d$ (lado opuesto al ángulo B): $\frac{d}{\sin(B)} = \frac{9}{\sin(C)}$
Sustituyendo los valores conocidos: $\frac{d}{\sin(50^\circ)} = \frac{9}{\sin(70^\circ)}$
-
Resolver para 'd' Despejamos $d$ de la ecuación: $d = \frac{9 \cdot \sin(50^\circ)}{\sin(70^\circ)}$
-
Calcular el valor de 'd' Usamos una calculadora para encontrar los valores de los senos y calcular $d$: $d = \frac{9 \cdot 0.766}{0.9397} \approx \frac{6.894}{0.9397} \approx 7.336$
Redondeando a dos decimales, obtenemos $d \approx 7.34$ km.
a) $7.33$ km
More Information
La Ley de los Senos es una herramienta muy útil para resolver triángulos cuando conocemos al menos un lado y dos ángulos, o dos lados y un ángulo opuesto a uno de ellos. En este caso, pudimos encontrar el tercer ángulo y luego usar la Ley de los Senos para hallar el lado desconocido.
Tips
Un error común es confundir la Ley de los Senos con la Ley de los Cosenos, o aplicar incorrectamente las razones trigonométricas. Asegúrate de identificar correctamente los lados y ángulos opuestos antes de aplicar la Ley de los Senos. Otro error común es usar la calculadora en modo incorrecto (grados vs. radianes).
AI-generated content may contain errors. Please verify critical information