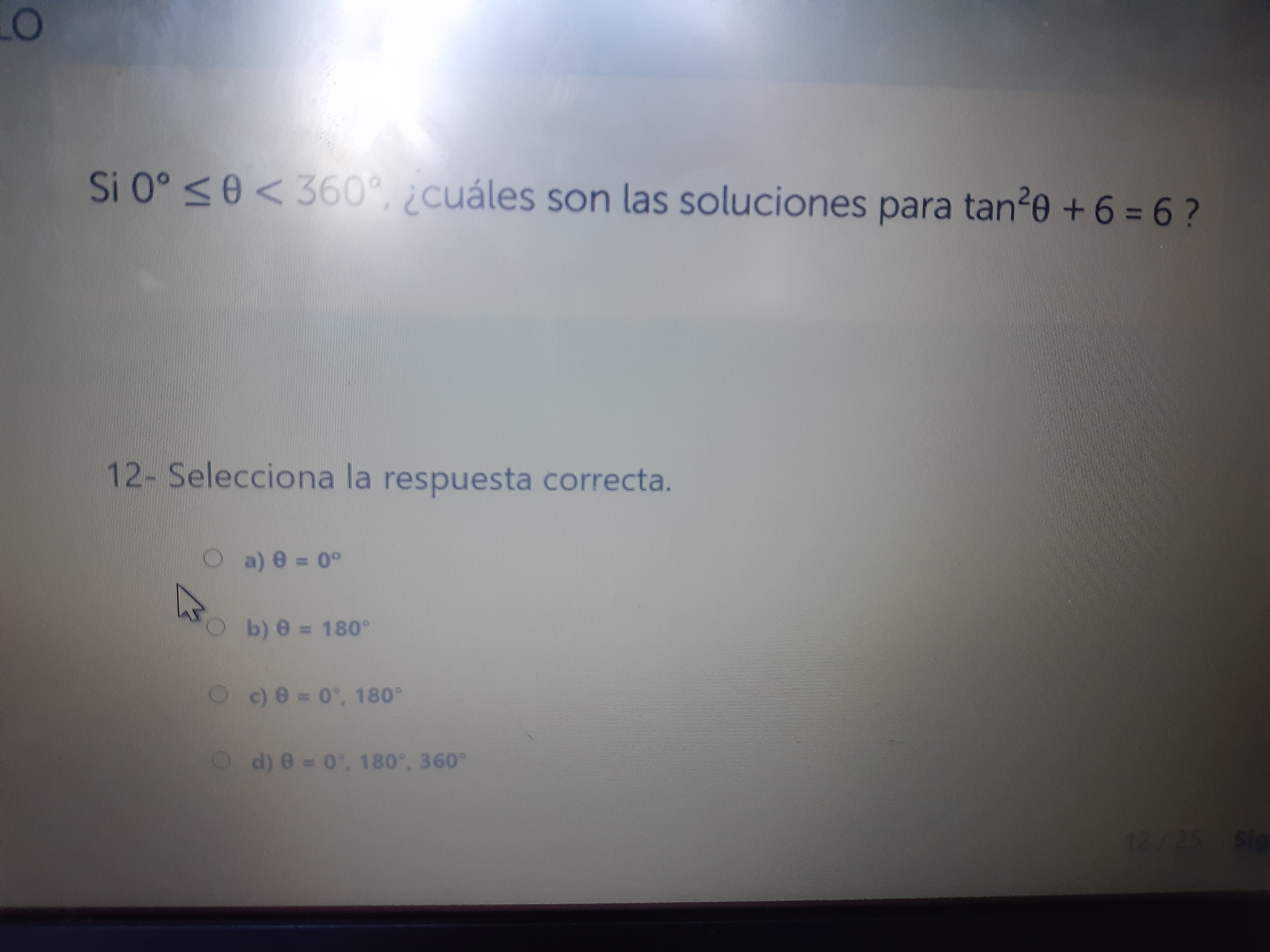
Si 0° ≤ θ < 360°, ¿cuáles son las soluciones para tan²θ + 6 = 6?
Understand the Problem
La pregunta pide encontrar las soluciones para la ecuación trigonométrica tan²θ + 6 = 6, dado que el ángulo θ está entre 0° y 360° (0° ≤ θ < 360°). Necesitamos simplificar la ecuación y encontrar los valores de θ que satisfacen la condición dada.
Answer
$ \theta = 0°, 180° $
Answer for screen readers
$ \theta = 0°, 180° $
Steps to Solve
-
Simplificar la ecuación Empezamos simplificando la ecuación original $$ \tan^2{\theta} + 6 =6$$ $$ \tan^2{\theta} = 6 - 6$$ $$ \tan^2{\theta} = 0$$
-
Encontrar tanθ Tomamos la raíz cuadrada en ambos lados para hallar $ \tan{\theta} $ $$ \sqrt{\tan^2{\theta}} = \sqrt{0} $$ $$ \tan{\theta} = 0$$
-
Hallar los ángulos donde tanθ = 0 Necesitamos encontrar los ángulos $ \theta $ entre $ 0° $ y $ 360° $ donde la tangente es 0. Sabemos que $ \tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}} $, entonces $ \tan{\theta} = 0 $ cuando $ \sin{\theta} = 0 $. Los ángulos donde $ \sin{\theta} = 0 $ son $ 0° $, $ 180° $ y $ 360° $.
-
Verificar el intervalo Dado que el problema especifica $ 0° \le \theta < 360° $, incluimos $ 0° $ y $ 180° $, pero excluimos $ 360° $.
-
Solución Por lo tanto, las soluciones son $ \theta = 0° $ y $ \theta = 180° $.
$ \theta = 0°, 180° $
More Information
La función tangente es cero en los múltiplos de $180°$.
Tips
El error común es excluir $0°$ o incluir $360°$ debido a la confusión con el intervalo dado.
AI-generated content may contain errors. Please verify critical information