Show that $2^{\ln x} = 3 - x$ has a solution in $[1, e]$.
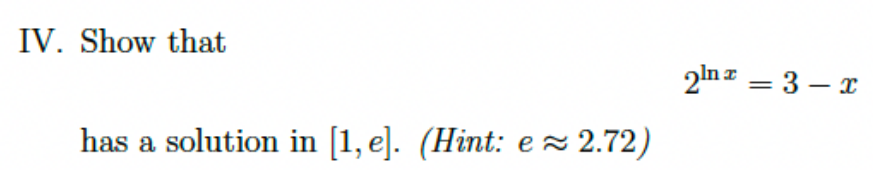
Understand the Problem
The question asks to show that the equation $2^{\ln x} = 3 - x$ has a solution in the interval $[1, e]$. This likely involves using the Intermediate Value Theorem (IVT) by defining a function, checking its continuity, and evaluating it at the endpoints of the interval.
Answer
Define $f(x) = 2^{\ln x} - (3 - x)$. Since $f(1) = -1 < 0$ and $f(e) = e - 1 > 0$, by the Intermediate Value Theorem, there exists a $c \in [1, e]$ such that $f(c) = 0$.
Answer for screen readers
There exists a solution in $[1, e]$ because $f(1) = -1$ and $f(e) = e - 1 > 0$. Since $f(x)$ is continuous on $[1,e]$ and the function changes sign on the interval, there exists $c \in [1,e]$ such that $f(c) = 0$.
Steps to Solve
- Define a function
Define a function $f(x) = 2^{\ln x} - (3 - x)$. We want to show that there exists a $c$ in $[1, e]$ such that $f(c) = 0$.
- Check for continuity
The function $f(x)$ is continuous on the interval $[1, e]$ since $2^{\ln x}$ and $3 - x$ are both continuous on this interval. The exponential function and logarithmic functions are continuous on their domains, and polynomials are continuous everywhere.
- Evaluate $f(x)$ at the endpoints of the interval
Evaluate $f(1)$ and $f(e)$:
$f(1) = 2^{\ln 1} - (3 - 1) = 2^0 - 2 = 1 - 2 = -1$ $f(e) = 2^{\ln e} - (3 - e) = 2^1 - (3 - e) = 2 - 3 + e = e - 1$
- Apply the Intermediate Value Theorem
Since $f(1) = -1 < 0$ and $f(e) = e - 1 > 0$ (because $e \approx 2.72 > 1$), and $f(x)$ is continuous on $[1, e]$, by the Intermediate Value Theorem, there exists a number $c$ in $(1, e)$ such that $f(c) = 0$. Therefore, the equation $2^{\ln x} = 3 - x$ has a solution in $[1, e]$.
There exists a solution in $[1, e]$ because $f(1) = -1$ and $f(e) = e - 1 > 0$. Since $f(x)$ is continuous on $[1,e]$ and the function changes sign on the interval, there exists $c \in [1,e]$ such that $f(c) = 0$.
More Information
The Intermediate Value Theorem (IVT) is a powerful tool for showing the existence of solutions to equations. To use IVT, you need to show that your function is continuous on a closed interval $[a, b]$ and that $f(a)$ and $f(b)$ have opposite signs. This guarantees the existence of at least one root in the open interval $(a, b)$.
Tips
A common mistake is to not explicitly state that the function is continuous before applying the Intermediate Value Theorem. Another common mistake is to incorrectly evaluate the function at the endpoints of the interval.
AI-generated content may contain errors. Please verify critical information