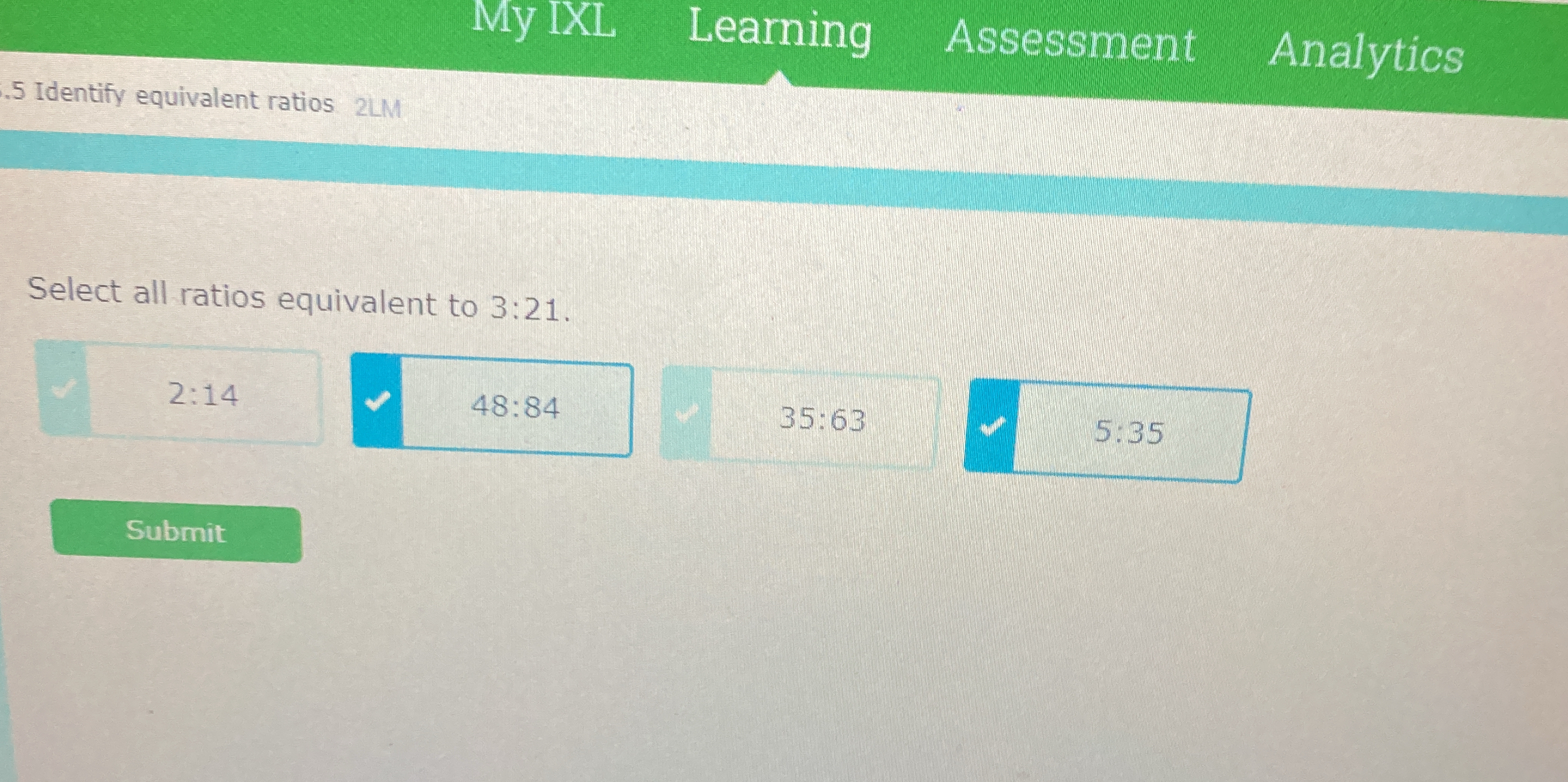
Select all ratios equivalent to 3:21.

Understand the Problem

The question is asking to identify which of the provided ratios are equivalent to the ratio 3:21. This requires understanding the concept of equivalent ratios and comparing each option provided.

Answer

The equivalent ratios to $3:21$ are $2:14$ and $5:35$.

Steps to Solve

Write the Given Ratio First, we have the ratio we want to investigate, which is $3:21$.
Simplify the Given Ratio To compare other ratios, we can simplify $3:21$ by dividing both numbers by their greatest common divisor (GCD), which is 3. $$ \frac{3}{3} : \frac{21}{3} = 1:7 $$
Simplify Each Ratio We then simplify each of the provided ratios in the same manner:
- For $2:14$: $$ \frac{2}{2} : \frac{14}{2} = 1:7 $$
- For $48:84$: $$ \frac{48}{12} : \frac{84}{12} = 4:7 $$
- For $35:63$: $$ \frac{35}{7} : \frac{63}{7} = 5:9 $$
- For $5:35$: $$ \frac{5}{5} : \frac{35}{5} = 1:7 $$
Compare Ratios Now, we compare the simplified ratios:

$1:7$ (for $2:14$) is equivalent to $1:7$ (original).
$4:7$ (for $48:84$) is not equivalent.
$5:9$ (for $35:63$) is not equivalent.
$1:7$ (for $5:35$) is equivalent to $1:7$ (original).

Identify the Equivalent Ratios The ratios that are equivalent to $3:21$ are $2:14$ and $5:35$.

The ratios equivalent to $3:21$ are $2:14$ and $5:35$.

More Information

Equivalent ratios are found by simplifying the ratios or multiplying/dividing both sides by the same number. Here, we simplified to see which matched the simplified form of the original ratio.

Tips

Not Simplifying Ratios: Sometimes, it is easy to skip the simplification step, which is crucial for correct comparison.
Misidentifying the GCD: Make sure to find the correct GCD when simplifying ratios; incorrect GCD can lead to wrong simplifications.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!