Resuelve para m<YBZ.
Understand the Problem
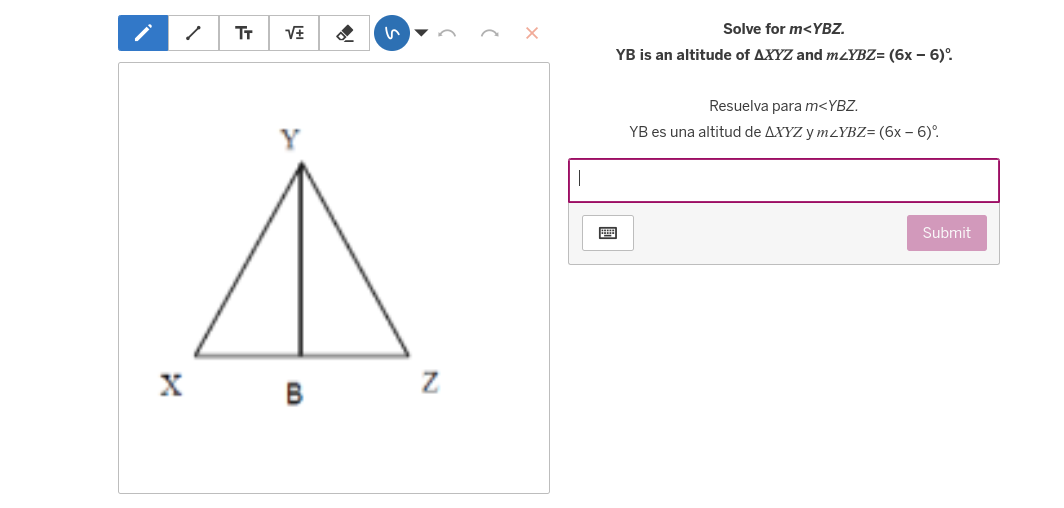
La pregunta está pidiendo resolver para el ángulo m<YBZ en el triángulo XYZ, donde YB es la altura y se proporciona la medida del ángulo como (6x - 6)°.
Answer
$m∠YBZ = 90°$
Answer for screen readers
$m∠YBZ = 90°$
Steps to Solve
-
Understanding the relationship between angles YB es la altura del triángulo XYZ. Esto implica que el triángulo YBZ es un triángulo rectángulo, donde el ángulo en B (m<YBZ) es un ángulo recto (90°) también. Por lo tanto, podemos usar la suma de los ángulos en el triángulo.
-
Usar la propiedad de los ángulos en un triángulo En cualquier triángulo, la suma de los ángulos es 180°. En el triángulo YBZ, tenemos: $$ m∠YBZ + m∠Y + m∠Z = 180° $$ Como sabemos que m<YBZ es un ángulo recto, entonces m<YBZ = 90°.
-
Sustituyendo valores Usando la información dada: $$ 90° + m∠Y + m∠Z = 180° $$ Podemos deducir que: $$ m∠Y + m∠Z = 90° $$
-
Sustitución del ángulo Según la pregunta, se especifica que m<YBZ es también igual a (6x - 6)°: $$ 90° = 6x - 6 $$
-
Resolviendo para x Para resolver la ecuación, sumamos 6 a ambos lados: $$ 90 + 6 = 6x $$ $$ 96 = 6x $$
Después, dividimos entre 6: $$ x = \frac{96}{6} = 16 $$
- Sustituyendo x para encontrar m<YBZ Finalmente, sustituimos x en la expresión original para m<YBZ: $$ m∠YBZ = 6(16) - 6 $$ $$ m∠YBZ = 96 - 6 = 90° $$
$m∠YBZ = 90°$
More Information
En un triángulo rectángulo, uno de los ángulos es siempre 90°. En este caso, hemos usado la propiedad de la suma de los ángulos de un triángulo para verificar que el ángulo YBZ coincide con el valor encontrado. Esto es esencial para resolver problemas de triángulos en geometría.
Tips
null
AI-generated content may contain errors. Please verify critical information