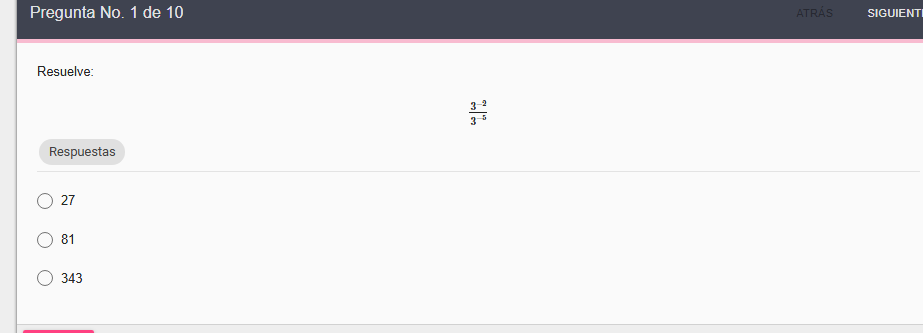
Resuelve: \frac{3^{-2}}{3^{-5}}
Understand the Problem
La pregunta está pidiendo resolver la expresión matemática \frac{3^{-2}}{3^{-5}}. Debemos aplicar las propiedades de las potencias para simplificar y encontrar el resultado.
Answer
$27$
Answer for screen readers
El resultado de la expresión es $27$.
Steps to Solve
- Aplicar la propiedad de cociente de potencias
La propiedad de cociente de potencias establece que se deben restar los exponentes cuando se divide una potencia por otra. Así que, podemos reescribir la expresión como:
$$ \frac{3^{-2}}{3^{-5}} = 3^{-2 - (-5)} = 3^{-2 + 5} $$
- Simplificar los exponentes
Ahora simplificamos el exponente resultante:
$$ -2 + 5 = 3 $$
Por lo tanto, la expresión se convierte en:
$$ 3^{3} $$
- Calcular el resultado final
Ahora calculamos el valor de $3^{3}$:
$$ 3^{3} = 27 $$
El resultado de la expresión es $27$.
More Information
El cálculo $3^{3}$ significa $3 \times 3 \times 3$, que es igual a $27$. Esta es una aplicación clásica de las propiedades de los exponentes.
Tips
- Confundir los signos al restar exponentes: Asegúrate de restar correctamente los exponentes; ten cuidado con los signos negativos.
- Olvidar que $a^{-n} = \frac{1}{a^{n}}$: Esto puede llevar a errores en los cálculos si se aplica incorrectamente.
AI-generated content may contain errors. Please verify critical information