Resuelva las siguientes ecuaciones: a) (2x - 1) / 4 = (8x - 4) / 1 b) √2x - (√2) / 1 = √8x
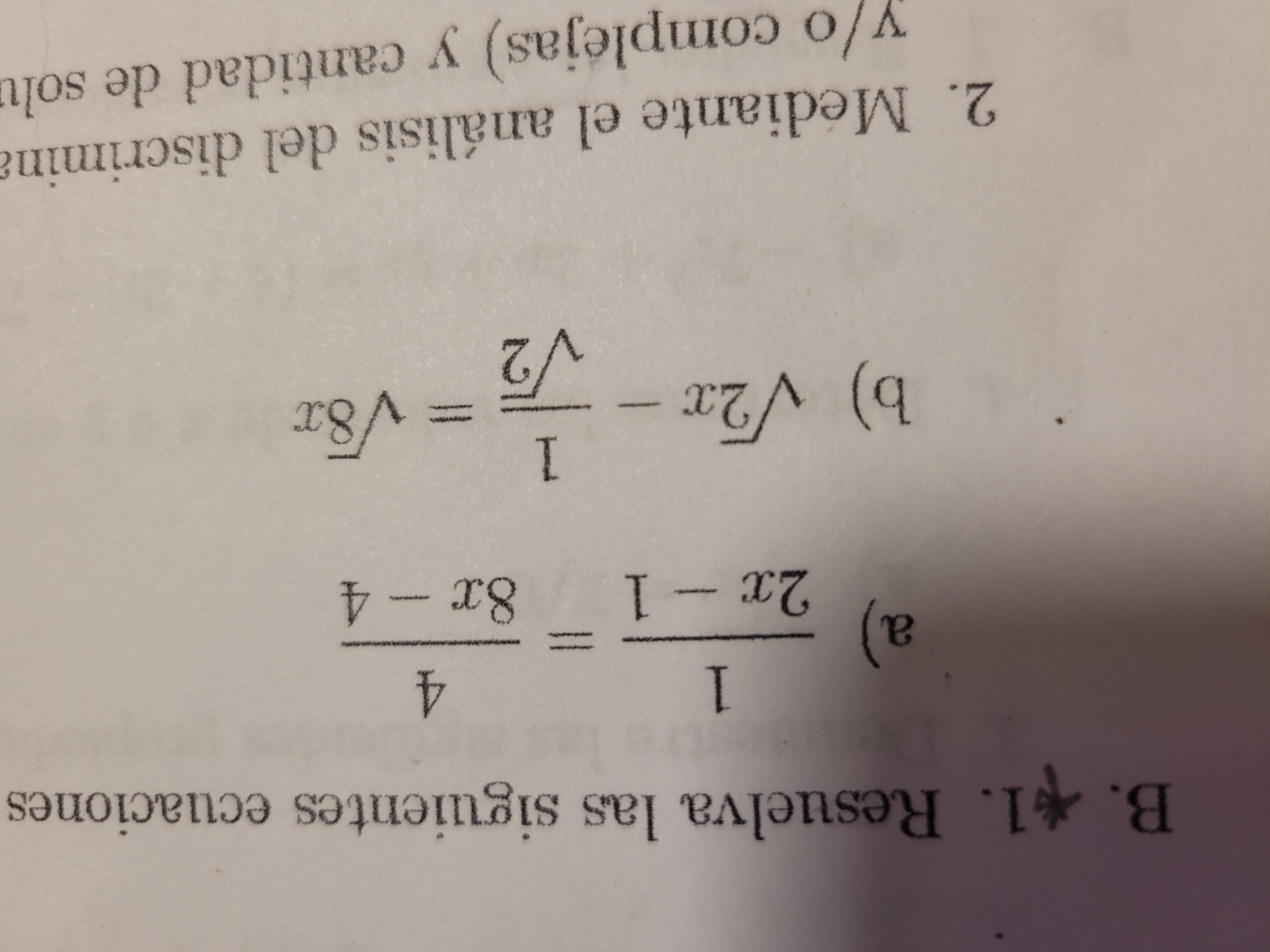
Understand the Problem
El problema consiste en resolver dos ecuaciones. La primera ecuación involucra una fracción algebraica y la segunda ecuación involucra términos con raíces cuadradas. Para resolverlas, debemos encontrar el valor o los valores de 'x' que satisfacen cada ecuación.
Answer
a) $x \in \mathbb{R}, x \neq \frac{1}{2}$ b) No hay solución.
Answer for screen readers
a) $x$ puede ser cualquier número real excepto $x = \frac{1}{2}$. b) No hay solución.
Steps to Solve
- Resolver la ecuación a)
La ecuación a) es: $$ \frac{2x-1}{1} = \frac{8x-4}{4} $$ Multiplicamos ambos lados de la ecuación por 4: $$ 4(2x-1) = 8x-4 $$ Distribuimos el 4 en el lado izquierdo: $$ 8x - 4 = 8x - 4 $$ Restamos $8x$ a ambos lados: $$ -4 = -4 $$ Esto significa que la ecuación es verdadera para cualquier valor de $x$, excepto aquellos que hacen que el denominador de la fracción original sea cero. En este caso, el denominador $8x-4$ es cero cuando $x = \frac{1}{2}$.
- Resolver la ecuación b)
La ecuación b) es: $$ \sqrt{2x} - \sqrt{2} = \sqrt{8x} $$ Reescribimos $\sqrt{8x}$ como $\sqrt{4 \cdot 2x} = 2\sqrt{2x}$: $$ \sqrt{2x} - \sqrt{2} = 2\sqrt{2x} $$ Restamos $\sqrt{2x}$ a ambos lados: $$ -\sqrt{2} = \sqrt{2x} $$ Elevamos al cuadrado ambos lados: $$ (-\sqrt{2})^2 = (\sqrt{2x})^2 $$ $$ 2 = 2x $$ Dividimos ambos lados por 2: $$ x = 1 $$ Verificamos la solución en la ecuación original: $$ \sqrt{2(1)} - \sqrt{2} = \sqrt{8(1)} $$ $$ \sqrt{2} - \sqrt{2} = \sqrt{8} $$ $$ 0 = \sqrt{8} $$ Esto es falso, por lo tanto no hay solución.
a) $x$ puede ser cualquier número real excepto $x = \frac{1}{2}$. b) No hay solución.
More Information
Para la ecuación a), dado que ambos lados de la ecuación son idénticos después de la simplificación y al despejar la variable $x$, esto significa que cualquier valor de $x$ satisfaría la ecuación. Sin embargo, debemos excluir cualquier valor de $x$ que haga que el denominador de la expresión original sea cero, porque eso haría que la expresión no esté definida.
Para la ecuación b), el hecho de elevar al cuadrado ambos lados de la ecuación puede introducir soluciones extrañas. Por lo tanto, es fundamental verificar la solución obtenida sustituyéndola de nuevo en la ecuación original, para garantizar que realmente satisfaga la ecuación original.
Tips
- En la ecuación a), olvidar verificar los valores de $x$ que hacen que el denominador sea cero.
- En la ecuación b), no verificar la solución obtenida después de elevar al cuadrado ambos lados de la ecuación.
- No simplificar las raíces cuadradas correctamente. Por ejemplo, $\sqrt{8x}$ puede simplificarse como $2\sqrt{2x}$.
- Errores al elevar al cuadrado las expresiones con raíces cuadradas.
AI-generated content may contain errors. Please verify critical information