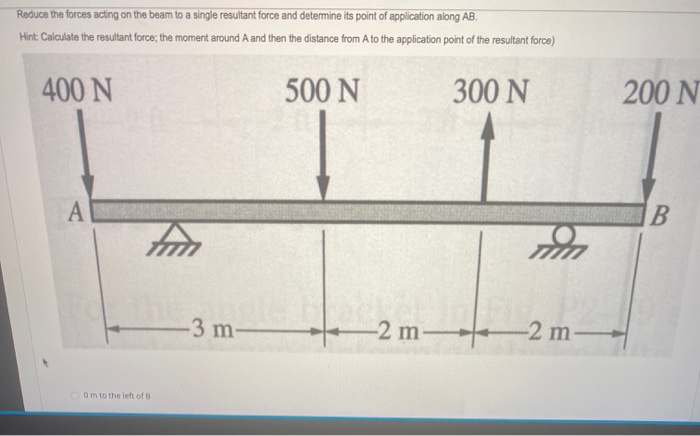
Reduce the forces acting on the beam to a single resultant force and determine its point of application along AB. Hint: Calculate the resultant force; the moment around A and then... Reduce the forces acting on the beam to a single resultant force and determine its point of application along AB. Hint: Calculate the resultant force; the moment around A and then the distance from A to the application point of the resultant force. Read more

Steps to Solve

1. Calculate the Resultant Force Add the magnitudes of all vertical forces acting on the beam. The total forces are:

• Upward forces: $500 , \text{N} + 300 , \text{N} + 200 , \text{N} = 1000 , \text{N}$
• Downward force: $400 , \text{N}$ Thus, the resultant force ($R$) is: $$ R = 1000 , \text{N} - 400 , \text{N} = 600 , \text{N} $$

2. Calculate the Moment about Point A The moment (torque) about point A can be calculated by considering the distances from A to each of the forces.

• For the $500 , \text{N}$ force: Moment = $500 , \text{N} \times 3 , \text{m} = 1500 , \text{Nm}$
• For the $300 , \text{N}$ force: Moment = $300 , \text{N} \times 5 , \text{m} = 1500 , \text{Nm}$
• For the $200 , \text{N}$ force: Moment = $200 , \text{N} \times 7 , \text{m} = 1400 , \text{Nm}$
• For the downward $400 , \text{N}$ force: Moment = $400 , \text{N} \times 0 , \text{m} = 0 , \text{Nm}$

Adding these moments (positive for counterclockwise, negative for clockwise): $$ M_A = 1500 , \text{Nm} + 1500 , \text{Nm} + 1400 , \text{Nm} - 0 , \text{Nm} = 3400 , \text{Nm} $$

3. Calculate the Moment of the Resultant Force We need to find the distance ($d$) from point A where the resultant force acts. The moment created by the resultant force ($R$) about point A is given by: $$ M_R = R \cdot d $$ Equating this to the total moment calculated before: $$ 3400 , \text{Nm} = 600 , \text{N} \cdot d $$

4. Solve for Distance $d$ Rearranging gives: $$ d = \frac{3400 , \text{Nm}}{600 , \text{N}} = \frac{3400}{600} \approx 5.67 , \text{m} $$

Since the total length of AB is $3 + 2 + 2 = 7 , \text{m}$, and the resulting distance indicates that the resultant force acts at approximately $5.67 , \text{m}$ from point A, which is within the beam.