Range of y = √(x² + 1) is:
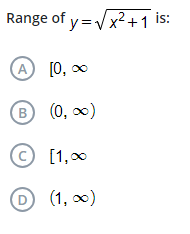
Understand the Problem
The question is asking for the range of the function y = √(x² + 1). The goal is to determine the set of possible output values (y-values) that the function can produce based on the given input values (x-values).
Answer
The range of $y = \sqrt{x^2 + 1}$ is $[1, \infty)$.
Answer for screen readers
The range of $y = \sqrt{x^2 + 1}$ is $[1, \infty)$.
Steps to Solve
-
Identify the function and its properties
The given function is $y = \sqrt{x^2 + 1}$. Recognize that the square root function always produces non-negative results. -
Analyze the expression inside the square root
The expression $x^2 + 1$ is always positive for all real numbers $x$ because $x^2$ is non-negative and the smallest value $x^2$ can achieve is 0. Therefore, the minimum value of $x^2 + 1$ is 1. -
Determine the minimum output of the function
Since the minimum value of $x^2 + 1$ is 1, taking the square root gives the minimum value of $y$:
$$\sqrt{1} = 1$$
Thus, the output $y$ must be at least 1. -
Determine the behavior as $x$ approaches infinity
As $x$ increases or decreases without bound, the value of $x^2 + 1$ also increases, causing $y$ to increase without limit. Thus, the maximum value of $y$ approaches infinity. -
State the range
From the analysis, the range of the function is determined to be from the minimum value of 1 upward to infinity:
$$[1, \infty)$$
The range of $y = \sqrt{x^2 + 1}$ is $[1, \infty)$.
More Information
The function $y = \sqrt{x^2 + 1}$ represents a hyperbola's upper half and its behavior indicates that it will never dip below 1, as the lowest point occurs at $x = 0$.
Tips
- Confusing the minimum value of the square root function by not recognizing that $x^2$ contributes to the value always being at least 1.
- Misinterpreting the interval notation; it's important to note whether the brackets indicate inclusive or exclusive bounds.
AI-generated content may contain errors. Please verify critical information