Understand the Problem
The question appears to deal with the concepts of physics involving forces and motion in a circular path, particularly focusing on dynamics that include tension, gravitational force, and acceleration components in a pendulum-like setup. It involves deriving equations and understanding the relationships between these variables.
Answer
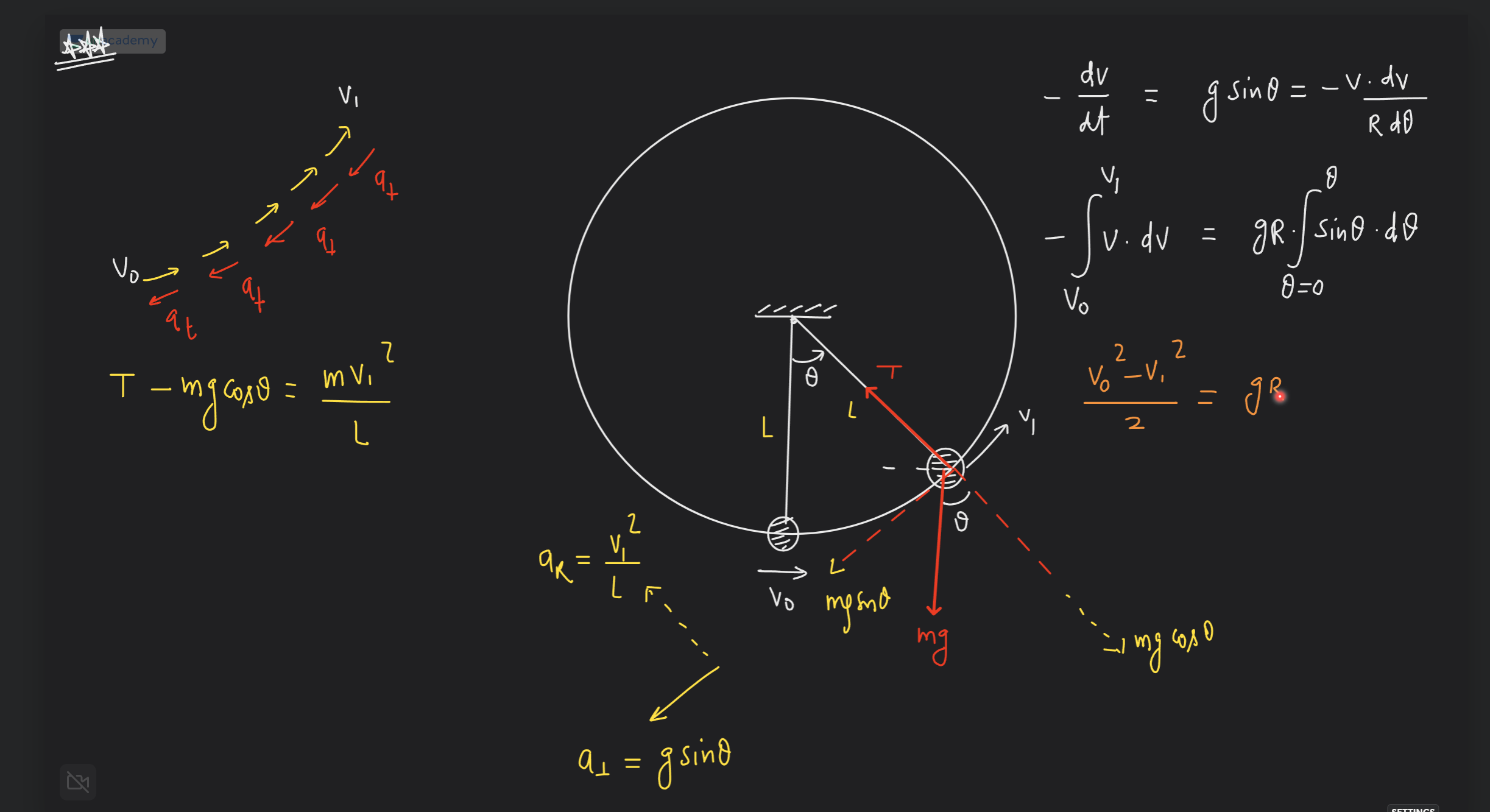
$$ T = \frac{mv_1^2}{L} + mg \cos \theta $$
Answer for screen readers
The expression for tension ( T ) in the pendulum system is given by: $$ T = \frac{mv_1^2}{L} + mg \cos \theta $$
Steps to Solve
-
Identify the forces acting on the mass The forces acting on the mass ( m ) in the pendulum motion are the tension ( T ) in the string and the gravitational force ( mg ). The component of the gravitational force acting along the direction of the string is ( mg \cos \theta ).
-
Write down the net force equation The net force acting on the mass can be expressed using Newton’s second law. The radial component of the forces gives: $$ T - mg \cos \theta = \frac{mv^2}{L} $$ This equation relates tension, gravitational force, and the centripetal force needed to keep the mass moving in a circular path.
-
Set up the equation for motion The tangential acceleration ( a_t ) can be defined as: $$ a_t = g \sin \theta $$ This will help in understanding the component of acceleration along the direction of motion.
-
Integrate to find velocities Using the relationship between acceleration and velocity, you can set up the integration: $$ - \int_{v_0}^{v_1} v , dv = -g R \int_0^{\theta} \sin \theta , d\theta $$ This establishes the connection between initial and final velocities with the angle swept during the motion.
-
Solve for change in velocity The integration yields: $$ \frac{v_0^2 - v_1^2}{2} = gR $$ Where ( R ) is the radius and gives an expression for the relationship between initial and final velocities in terms of gravitational acceleration.
-
Substitute initial and final velocities to determine tension From the net force equation, you can substitute ( v_1 ) to find tension ( T ): $$ T = \frac{mv_1^2}{L} + mg \cos \theta $$
The expression for tension ( T ) in the pendulum system is given by: $$ T = \frac{mv_1^2}{L} + mg \cos \theta $$
More Information
This formulation is essential in understanding dynamics in circular motion, especially in systems like pendulums. It illustrates how tension in the string adjusts based on the velocity of the mass and the angle with respect to the vertical.
Tips
- Ignoring the components of forces: Remember to break down forces into components along and perpendicular to the motion.
- Misapplying conservation of energy principles: Ensure that kinetic and potential energies are properly accounted for when changing states.
AI-generated content may contain errors. Please verify critical information