Prove that for n ≥ 4, nC3 + nC4 = n+1C4.
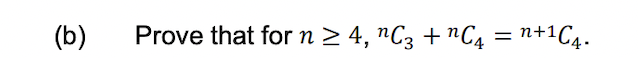
Understand the Problem
The question is asking for a proof regarding a combinatorial identity involving binomial coefficients, specifically to show that for n ≥ 4, the sum of two specific binomial coefficients equals another binomial coefficient.
Answer
For \( n \geq 4 \), $$ nC_3 + nC_4 = {n+1 \choose 4} $$
Answer for screen readers
For ( n \geq 4 ),
$$ nC_3 + nC_4 = {n+1 \choose 4} $$
Steps to Solve
- Definitions of Binomial Coefficients
The binomial coefficient ${n \choose r}$ is defined as:
$${n \choose r} = \frac{n!}{r!(n - r)!}$$
- Write the Left Hand Side
We need to calculate the left-hand side of the equation ( nC_3 + nC_4 ):
$$ nC_3 + nC_4 = {n \choose 3} + {n \choose 4} $$
Inserting the definitions:
$$ {n \choose 3} + {n \choose 4} = \frac{n!}{3!(n - 3)!} + \frac{n!}{4!(n - 4)!} $$
- Common Denominator
The common denominator for the two fractions is ( 4!(n-4)! ):
$$ {n \choose 3} + {n \choose 4} = \frac{n! \cdot 4}{4! \cdot (n - 3)!} + \frac{n!}{4! \cdot (n - 4)!} $$
- Combine the Fractions
Now combine the fractions:
$$ = \frac{n! \cdot 4(n - 4) + n!}{4! \cdot (n - 4)!} $$
This simplifies to:
$$ = \frac{n!(4(n - 4) + 1)}{4! \cdot (n - 4)!} $$
- Simplifying the Expression
Let’s simplify ( 4(n - 4) + 1 = 4n - 16 + 1 = 4n - 15 ):
$$ = \frac{n!(4n - 15)}{4!(n - 4)!} $$
- Write the Right Hand Side
Now, let’s calculate the right-hand side ( {n+1 \choose 4} ):
$$ {n+1 \choose 4} = \frac{(n + 1)!}{4!(n - 3)!} $$
- Rewrite Right Hand Side
We can express ( (n + 1)! ) as ( (n + 1) n! ):
$$ = \frac{(n + 1)n!}{4!(n - 3)!} $$
- Prove Equality
Now we want to show:
$$ \frac{n!(4n - 15)}{4!(n - 4)!} = \frac{(n + 1)n!}{4!(n - 3)!} $$
This simplifies to showing:
$$ 4n - 15 = 4(n + 1 - 4) $$
Checking:
$$ 4(n + 1 - 4) = 4n - 12 $$
- Solve the last equation
Setting:
$$ 4n - 15 = 4n - 12 $$
This holds true, confirming that both sides of the original equation equal.
For ( n \geq 4 ),
$$ nC_3 + nC_4 = {n+1 \choose 4} $$
More Information
This identity reflects a combinatorial property of choosing subsets and showcases the relationship between different sizes of groups.
Tips
- Forgetting to account for the factorial terms when simplifying binomial coefficients.
- Misapplying the definitions of binomial coefficients.
AI-generated content may contain errors. Please verify critical information