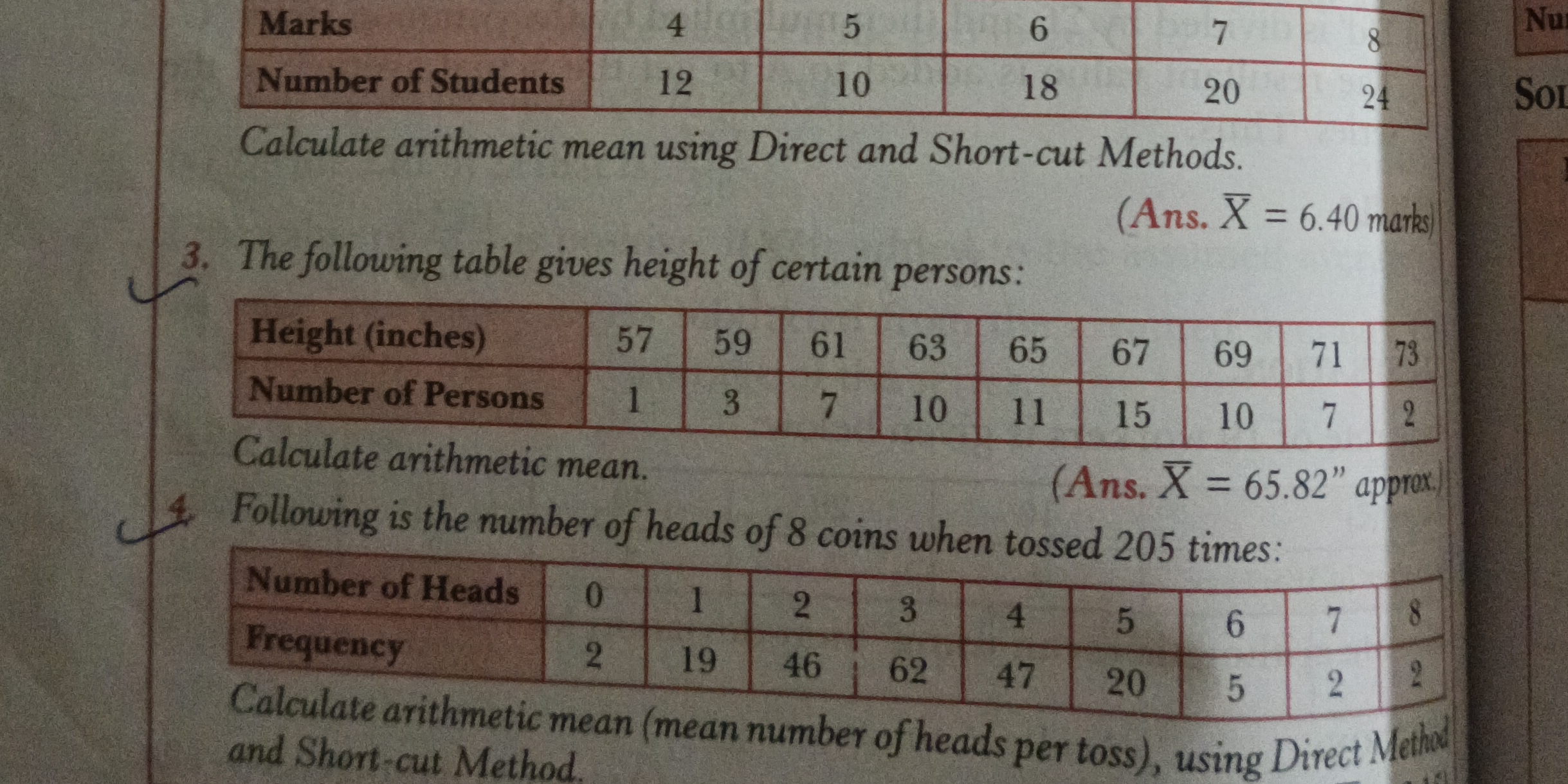
Problem 3: The following table gives the height of certain persons. Calculate the arithmetic mean. | Height (inches) | 57 | 59 | 61 | 63 | 65 | 67 | 69 | 71 | 73 | |---|---|---|--... Problem 3: The following table gives the height of certain persons. Calculate the arithmetic mean. | Height (inches) | 57 | 59 | 61 | 63 | 65 | 67 | 69 | 71 | 73 | |---|---|---|---|---|---|---|---|---|---| | Number of Persons | 1 | 3 | 7 | 10 | 11 | 15 | 10 | 7 | 2 | Problem 4: Following is the number of heads of 8 coins when tossed 205 times. Calculate the arithmetic mean (mean number of heads per toss), using the Direct Method and Short-cut Method. | Number of Heads | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |---|---|---|---|---|---|---|---|---|---| | Frequency | 2 | 19 | 46 | 62 | 47 | 20 | 5 | 2 | 2 | Read more

Steps to Solve

Here are the step-by-step solutions for both problems:

Problem 3: Calculating the arithmetic mean height

1. Multiply each height by the number of persons with that height. This will give the total height contributed by people of each height.

   • $57 \times 1 = 57$
   • $59 \times 3 = 177$
   • $61 \times 7 = 427$
   • $63 \times 10 = 630$
   • $65 \times 11 = 715$
   • $67 \times 15 = 1005$
   • $69 \times 10 = 690$
   • $71 \times 7 = 497$
   • $73 \times 2 = 146$

2. Sum the products calculated in the previous step. This gives the total height of all persons.

   $57 + 177 + 427 + 630 + 715 + 1005 + 690 + 497 + 146 = 4344$

3. Sum the number of persons. This gives the total number of persons.

   $1 + 3 + 7 + 10 + 11 + 15 + 10 + 7 + 2 = 66$

4. Divide the total height (step 2) by the total number of persons (step 3). This gives the arithmetic mean height.

   $\frac{4344}{66} = 65.8181... \approx 65.82$

Problem 4: Calculating the arithmetic mean number of heads

Direct Method

1. Multiply each number of heads by its frequency.

   • $0 \times 2 = 0$
   • $1 \times 19 = 19$
   • $2 \times 46 = 92$
   • $3 \times 62 = 186$
   • $4 \times 47 = 188$
   • $5 \times 20 = 100$
   • $6 \times 5 = 30$
   • $7 \times 2 = 14$
   • $8 \times 2 = 16$

2. Sum the products calculated in the previous step.

   $0 + 19 + 92 + 186 + 188 + 100 + 30 + 14 + 16 = 645$

3. Sum the frequencies. This gives the total number of tosses.

   $2 + 19 + 46 + 62 + 47 + 20 + 5 + 2 + 2 = 205$

4. Divide the sum of the products (step 2) by the sum of the frequencies (step 3). This gives the arithmetic mean.

   $\frac{645}{205} = 3.1463 \approx 3.15$

Short-cut Method

1. Choose an assumed mean. Let's choose $A = 3$.

2. Calculate the deviation $d_i = x_i - A$ for each $x_i$ (number of heads).

   • $0 - 3 = -3$
   • $1 - 3 = -2$
   • $2 - 3 = -1$
   • $3 - 3 = 0$
   • $4 - 3 = 1$
   • $5 - 3 = 2$
   • $6 - 3 = 3$
   • $7 - 3 = 4$
   • $8 - 3 = 5$

3. Multiply each deviation by its corresponding frequency.

   • $-3 \times 2 = -6$
   • $-2 \times 19 = -38$
   • $-1 \times 46 = -46$
   • $0 \times 62 = 0$
   • $1 \times 47 = 47$
   • $2 \times 20 = 40$
   • $3 \times 5 = 15$
   • $4 \times 2 = 8$
   • $5 \times 2 = 10$

4. Sum the products from step 3.

   $-6 - 38 - 46 + 0 + 47 + 40 + 15 + 8 + 10 = 30$

5. Sum the frequencies. (Same as in the direct method)

   $2 + 19 + 46 + 62 + 47 + 20 + 5 + 2 + 2 = 205$

6. Calculate the mean using the formula: $\text{Mean} = A + \frac{\sum f_i d_i}{\sum f_i}$

   $\text{Mean} = 3 + \frac{30}{205} = 3 + 0.1463 \approx 3.1463 \approx 3.15$