Pomocou Greenovej vety vypočítajme ∮(2e^{2x} ext{sin} y - 6)dx + (e^{2x} ext{cos} y + 4x)dy.
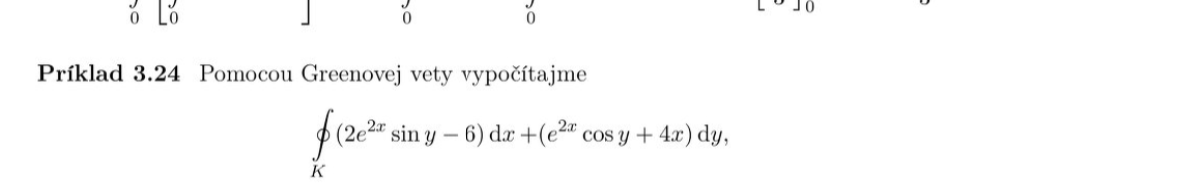
Understand the Problem
Otázka sa pýta, ako použiť Greenovu vetu na výpočet určitého integrálu v uvedenom výraze. Základný prístup zahŕňa identifikáciu potrebných funkcií a aplikuje veci z teórie vektorového kalkulu na konečné krivky.
Answer
Konečný výsledok integrálu je $4$.
Answer for screen readers
Konečný výsledok integrálu je: [ \oint_C (2e^{2x} \sin y - 6)dx + (e^{2x} \cos y + 4x)dy = 4 ]
Steps to Solve
-
Identifikácia funkcií Identifikujeme funkcie $P(x,y)$ a $Q(x,y)$ z daného integrálu. Tu sú: [ P(x,y) = 2e^{2x} \sin y - 6 ] [ Q(x,y) = e^{2x} \cos y + 4x ]
-
Výpočet parciálnych derivácií Vypočítame parciálne derivácie $P$ a $Q$: [ \frac{\partial Q}{\partial x} = 2e^{2x} \cos y + 4 ] [ \frac{\partial P}{\partial y} = 2e^{2x} \cos y ]
-
Aplikácia Greenovej vety Podľa Greenovej vety môžeme premeniť obvodový integrál na dvojitý integrál: [ \oint_C (P,dx + Q,dy) = \iint_R \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) dA ]
-
Výpočet dvojitého integrálu Teraz vypočítame: [ \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} = (2e^{2x} \cos y + 4) - (2e^{2x} \cos y) = 4 ] Pre dvojitý integrál cez oblasť $R$, ktorá je v tomto prípade štvorcový oblasť s vrcholmi $(0,0)$ a $(1,1)$, máme: [ \iint_R 4 , dA = 4 \cdot \text{area of } R = 4 \cdot 1 = 4 ]
Konečný výsledok integrálu je: [ \oint_C (2e^{2x} \sin y - 6)dx + (e^{2x} \cos y + 4x)dy = 4 ]
More Information
Greenova veta, známa v teórii vektorového kalkulu, nám umožňuje previesť obvodový integrál na dvojitý integrál. Tento spôsob je užitočný na zjednodušenie výpočtov a zobrazuje vzťah medzi obvodmi a obsahom.
Tips
- Nezabudnúť správne vypočítať parciálne derivácie $P$ a $Q$.
- Zapamätať si, že oblasť $R$ je definovaná správne, najmä v prípade rôznych tvarov oblastí.
- Nesprávne aplikovanie Greenovej vety, čo môže viesť k chybnému hodnoteniu integrálu.
AI-generated content may contain errors. Please verify critical information