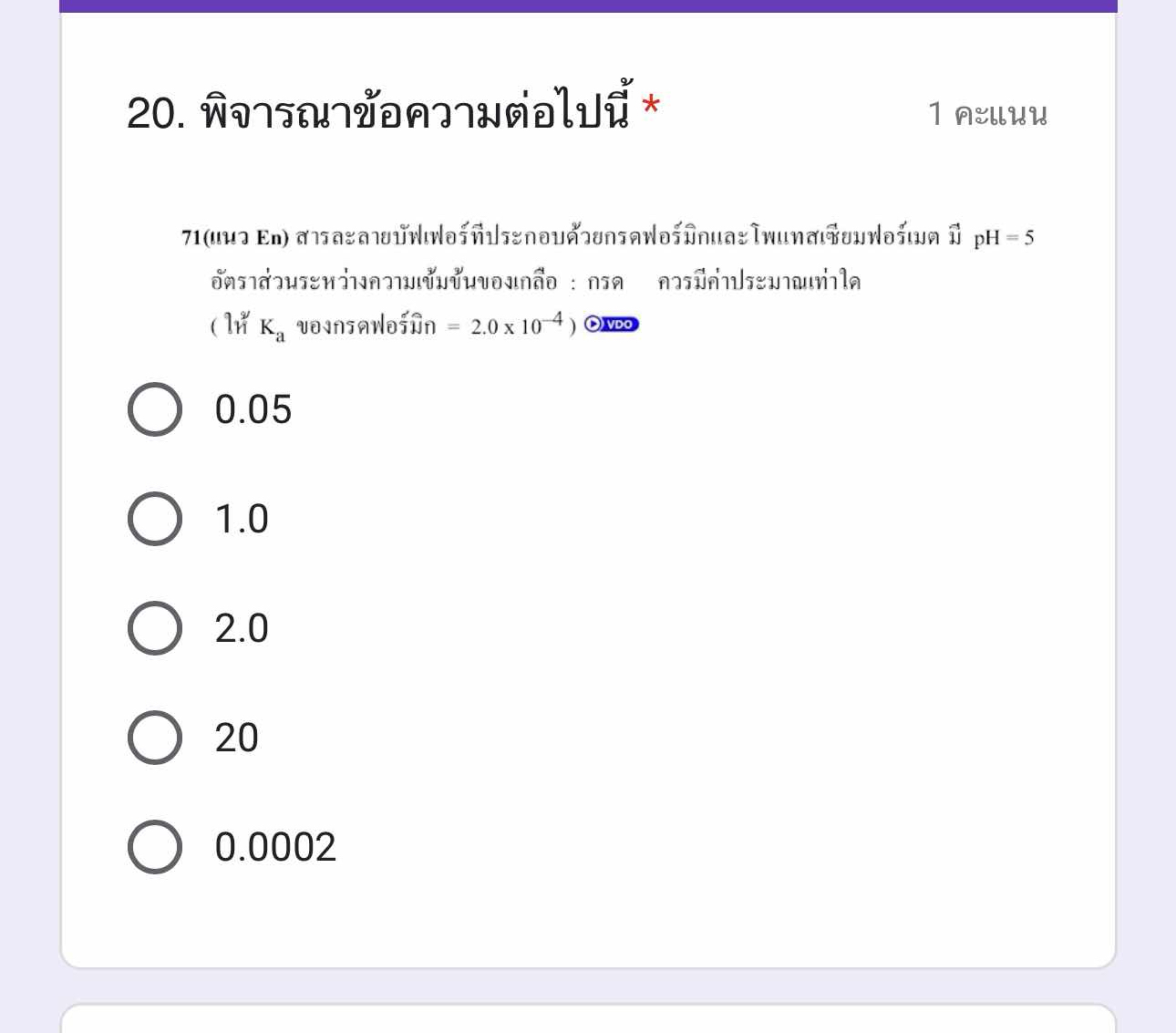
สารละลายบัฟเฟอร์ที่ประกอบด้วยกรดฟอร์มิกและโพแทสเซียมฟอร์เมต มี pH = 5 อัตราส่วนระหว่างความเข้มข้นของเกลือ : กรด ควรมีค่าประมาณเท่าใด (ให้ Kₐ ของกรดฟอร์มิก = 2.0 x 10⁻⁴) สารละลายบัฟเฟอร์ที่ประกอบด้วยกรดฟอร์มิกและโพแทสเซียมฟอร์เมต มี pH = 5 อัตราส่วนระหว่างความเข้มข้นของเกลือ : กรด ควรมีค่าประมาณเท่าใด (ให้ Kₐ ของกรดฟอร์มิก = 2.0 x 10⁻⁴) Read more

Steps to Solve

1. Understanding the Henderson-Hasselbalch Equation

The Henderson-Hasselbalch equation relates the pH of a buffer solution to the $pK_a$ of the acid and the ratio of the concentrations of the conjugate base (salt) and the acid. The equation is:

$pH = pK_a + log(\frac{[salt]}{[acid]})$

2. Calculate $pK_a$

We are given that $K_a = 2.0 \times 10^{-4}$. We need to find $pK_a$, which is the negative logarithm (base 10) of $K_a$:

$pK_a = -log(K_a) = -log(2.0 \times 10^{-4})$ $pK_a = -log(2.0) - log(10^{-4}) = -0.301 - (-4) = 4 - 0.301 = 3.699 \approx 3.7$

3. Using the Henderson-Hasselbalch Equation to find the ratio $\frac{[salt]}{[acid]}$

We are given that $pH = 5$. Plug in $pH$ and the value of $pK_a$ into the Henderson-Hasselbalch equation to solve for the ratio $\frac{[salt]}{[acid]}$:

$5 = 3.7 + log(\frac{[salt]}{[acid]})$ $log(\frac{[salt]}{[acid]}) = 5 - 3.7 = 1.3$

4. Solve for the ratio

To find the ratio $\frac{[salt]}{[acid]}$, we need to take the antilog (10 to the power of) of both sides:

$\frac{[salt]}{[acid]} = 10^{1.3} \approx 20$