Perform the operation. (10x^2 + 8x - 5) - (-9x^2 - 3x - 4)
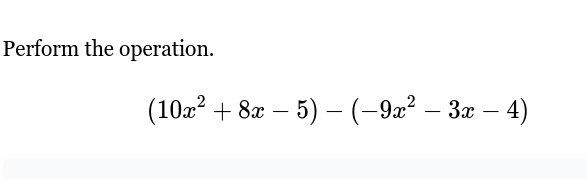
Understand the Problem
The question asks us to simplify the expression by performing the subtraction operation between two polynomials. We need to combine like terms after distributing the negative sign.
Answer
$19x^2 + 11x - 1$
Answer for screen readers
$19x^2 + 11x - 1$
Steps to Solve
- Distribute the negative sign Distribute the negative sign in front of the second polynomial to each term inside the parentheses.
$(10x^2 + 8x - 5) - (-9x^2 - 3x - 4) = 10x^2 + 8x - 5 + 9x^2 + 3x + 4$
- Combine like terms Combine the terms with the same variable and exponent.
$(10x^2 + 9x^2) + (8x + 3x) + (-5 + 4) = 19x^2 + 11x - 1$
$19x^2 + 11x - 1$
More Information
Polynomial subtraction is similar to polynomial addition, but we need to distribute the negative sign before combining like terms.
Tips
A common mistake is forgetting to distribute the negative sign to all terms in the second polynomial. For example, some might only change the sign of the first term and not the others, leading to an incorrect answer.
AI-generated content may contain errors. Please verify critical information