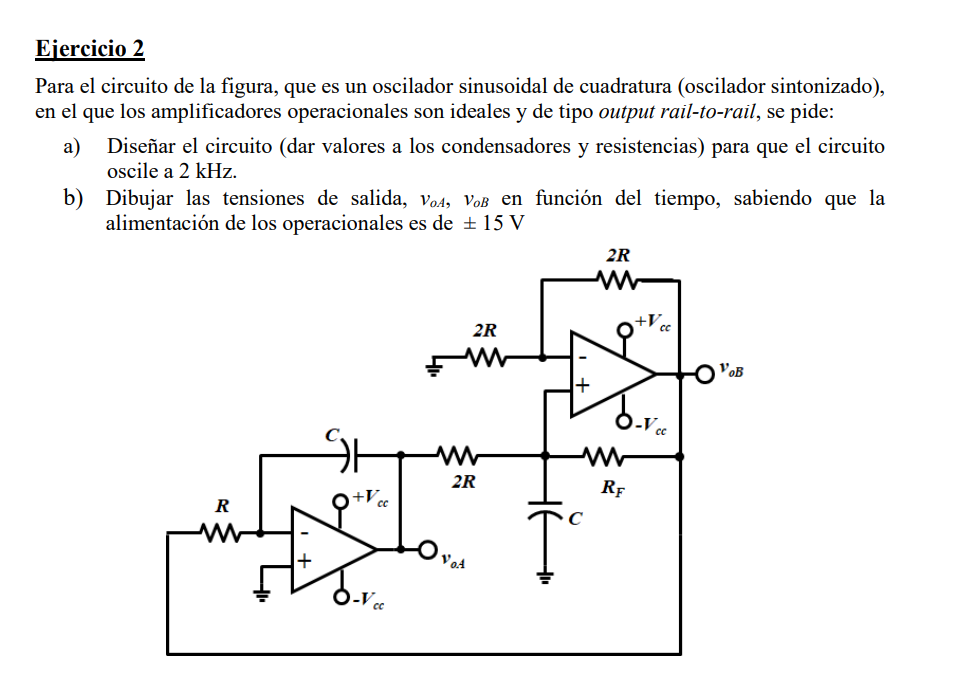
Para el circuito de la figura, que es un oscilador sinusoidal de cuadratura, se pide: a) Diseñar el circuito para que oscile a 2 kHz. b) Dibujar las tensiones de salida, voA, voB e... Para el circuito de la figura, que es un oscilador sinusoidal de cuadratura, se pide: a) Diseñar el circuito para que oscile a 2 kHz. b) Dibujar las tensiones de salida, voA, voB en función del tiempo, sabiendo que la alimentación de los operacionales es de ± 15 V.
Understand the Problem
La pregunta pide diseñar un circuito oscilador sinusoidal de cuadratura y dibujar las tensiones de salida en función del tiempo. Se deben proporcionar valores para los componentes y mostrar cómo variarán las tensiones de salida dado un suministro de ±15 V.
Answer
Valores seleccionados son $R = 10k\Omega$, $C \approx 7.96 \mu F$, $R_f = 20k\Omega$; las tensiones de salida son $v_{oA}(t) = 15 \sin(2\pi (2000) t)$ y $v_{oB}(t) = 15 \cos(2\pi (2000) t)$.
Answer for screen readers
Los valores seleccionados son:
- $R = 10k\Omega$
- $C \approx 7.96 \mu F$
- $R_f = 20k\Omega$
Las tensiones de salida son:
$$ v_{oA}(t) = 15 \sin(2\pi (2000) t) $$
$$ v_{oB}(t) = 15 \cos(2\pi (2000) t) $$
Steps to Solve
- Definir la frecuencia del oscilador
La frecuencia de oscilación $f$ está dada por la fórmula:
$$ f = \frac{1}{2\pi R C} $$
Sustituyendo $f = 2000$ Hz, podemos despejar una relación entre las resistencias y capacitancias.
- Calcular el valor de los componentes
Si elegimos un valor para $R$, podemos calcular $C$ utilizando la frecuencia deseada:
$$ C = \frac{1}{2 \pi R f} $$
Por ejemplo, si seleccionamos $R = 10k\Omega$, entonces:
$$ C = \frac{1}{2 \pi (10 \times 10^3) (2000)} \approx 7.96 \mu F $$
- Seleccionar el valor de $R_f$
Para completar el circuito, típicamente se escoge $R_f = 2R$, por lo tanto:
$$ R_f = 2 \times 10k\Omega = 20k\Omega $$
- Dibujar las señales de salida
Se dibujan las tensiones de salida $v_{oA}$ y $v_{oB}$ en función del tiempo. Para un oscilador en cuadratura, podemos mostrar que:
- $v_{oA}(t) = V_{max} \sin(2\pi f t)$
- $v_{oB}(t) = V_{max} \cos(2\pi f t)$
- Graficar las señales
El siguiente paso es graficar las señales de salida. Ambas señales tendrán amplitudes que oscilan entre ±15 V.
Los valores seleccionados son:
- $R = 10k\Omega$
- $C \approx 7.96 \mu F$
- $R_f = 20k\Omega$
Las tensiones de salida son:
$$ v_{oA}(t) = 15 \sin(2\pi (2000) t) $$
$$ v_{oB}(t) = 15 \cos(2\pi (2000) t) $$
More Information
En este circuito, el oscilador de cuadratura produce dos señales senoidales que están desfasadas 90 grados entre sí. La elección de R y C afecta la frecuencia de oscilación. Utilizando componentes estándar ayudará en la construcción del circuito.
Tips
- No usar valores estándar para resistencias y capacitores: Asegúrate de seleccionar componentes que estén disponibles comercialmente.
- Olvidar considerar el rango de alimentación: El circuito debe ser diseñado para operar correctamente dentro de la alimentación de ±15 V.
- Problemas con el desfase: Asegúrate de que las funciones seno y coseno sean correctamente identificadas en la salida.
AI-generated content may contain errors. Please verify critical information