OC = 6 cm y OB = 2 cm. ¿Cuánto vale FE/AB?
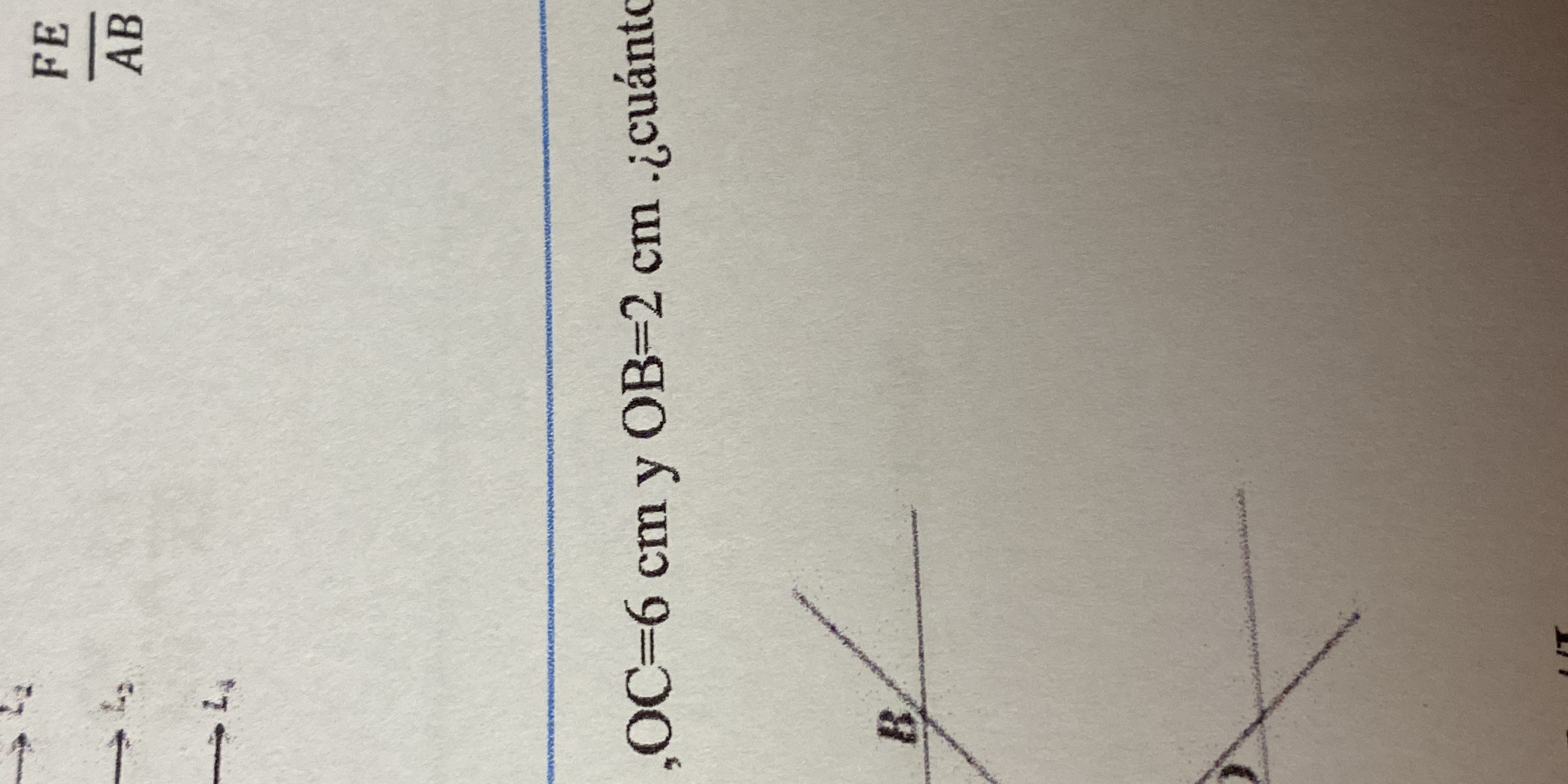
Understand the Problem
La pregunta nos pide calcular algo dada información sobre las longitudes de segmentos OC y OB. Probablemente se necesita determinar la longitud de algún otro segmento en la figura o alguna relación entre segmentos, basado en principios geométricos.
Answer
$ \frac{FE}{AB} = 3 $
Answer for screen readers
$ \frac{FE}{AB} = 3 $
Steps to Solve
-
Identify Similar Triangles From the image we can see that $ \triangle OAB $ and $ \triangle OFE $ are similar triangles, due to the parallel lines L1, L2 and L3.
-
Determine the Ratios of Corresponding Sides Since the triangles are similar, the ratios of their corresponding sides are equal. In particular, we have $ \frac{FE}{AB} = \frac{OF}{OA} = \frac{OE}{OB} $
-
Focus on the Relevant Ratio We are interested in $ \frac{FE}{AB} $, and we are given $OC = 6$ cm and $OB = 2$ cm. From the diagram we observe that $OE = OC = 6$ cm and $OB = 2$ cm.
-
Set up the Equation Then, $\frac{FE}{AB} = \frac{OE}{OB} = \frac{OC}{OB} $
-
Substitute the given values $ \frac{FE}{AB} = \frac{6}{2} $
-
Simplify the Expression $ \frac{FE}{AB} = 3 $
$ \frac{FE}{AB} = 3 $
More Information
The ratio of the sides FE and AB is 3. This indicates that FE is three times longer than AB.
Tips
- Confusing which sides correspond to each other in the similar triangles.
- Incorrectly setting up the ratios.
- Arithmetic errors when simplifying the fraction.
AI-generated content may contain errors. Please verify critical information