ω² + H₀ - 72 = 0
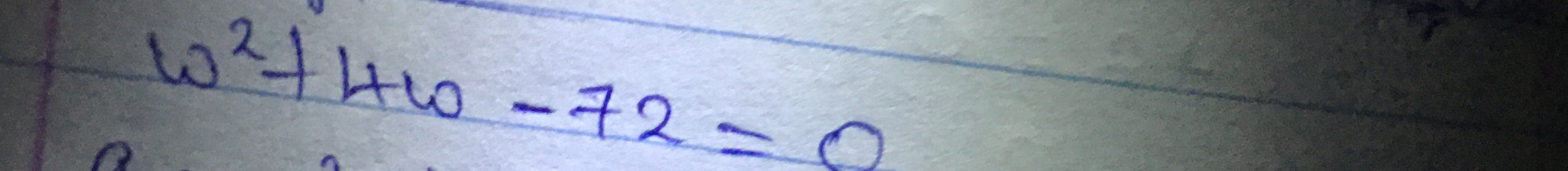
Understand the Problem
The question involves solving an equation of the form ω² + H₀ - 72 = 0. We're tasked with finding the value of ω given the equation.
Answer
$$ ω = ±\sqrt{72 - H₀} $$
Answer for screen readers
The value of $ω$ is given by: $$ ω = ±\sqrt{72 - H₀} $$
Steps to Solve
-
Rearrange the Equation To solve for $ω$, we need to rearrange the equation such that all terms involving $ω$ are on one side. Starting with the equation: $$ ω² + H₀ - 72 = 0 $$ we can rearrange it to: $$ ω² = 72 - H₀ $$
-
Solve for ω Now that we have $ω²$ isolated, we can take the square root of both sides to solve for $ω$. Note that we need to consider both the positive and negative square roots: $$ ω = ±\sqrt{72 - H₀} $$
-
Example Calculation If we substitutes a specific value for $H₀$, for instance, let’s say $H₀ = 8$: $$ ω = ±\sqrt{72 - 8} = ±\sqrt{64} = ±8 $$
The value of $ω$ is given by: $$ ω = ±\sqrt{72 - H₀} $$
More Information
This solution showcases that the variable $ω$ can take on two values (positive and negative) depending on the value of $H₀$. The specific answer will change with different values of $H₀$.
Tips
- Ignoring the ± sign: When taking the square root, not considering both the positive and negative values for $ω$ can lead to incomplete solutions.
- Miscalculation: An arithmetic error when substituting values can yield incorrect results.
AI-generated content may contain errors. Please verify critical information