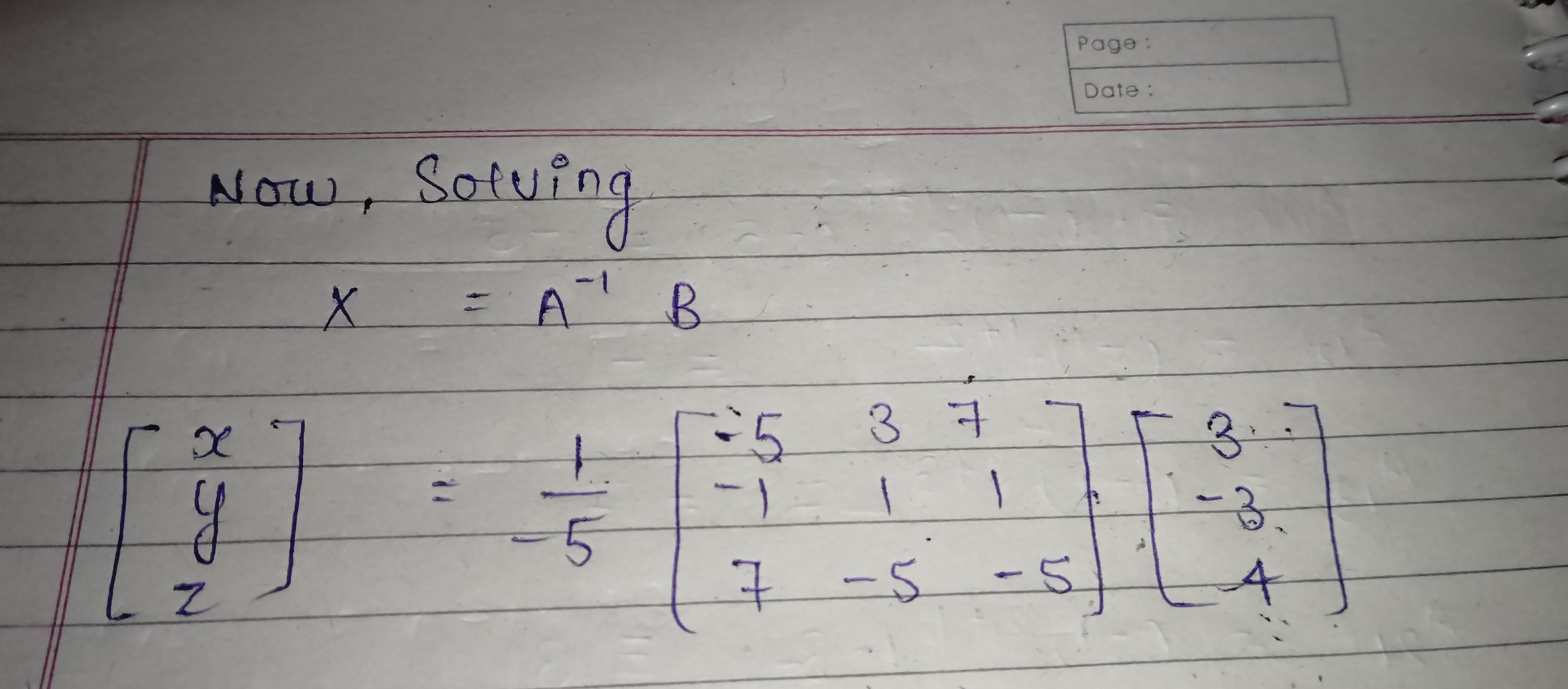
Now, solving X = A^(-1) B where A = [[-5, 3, 7], [-1, 1, 1], [7, -5, -5]] and B = [[3], [-3], [4]].
Understand the Problem
The question presents a matrix equation involving the inverse of a matrix A, which is being multiplied by another matrix B to solve for the variable matrix X. We need to perform matrix operations to find the values of x, y, and z.
Answer
$$ \begin{bmatrix} -\frac{4}{5} \\ \frac{2}{5} \\ -\frac{16}{5} \end{bmatrix} $$
Answer for screen readers
$$ \begin{bmatrix} x \ y \ z \end{bmatrix}
\begin{bmatrix} -\frac{4}{5} \ \frac{2}{5} \ -\frac{16}{5} \end{bmatrix} $$
Steps to Solve
-
Write down the matrix equation
The equation is given as: $$ \begin{bmatrix} x \ y \ z \end{bmatrix} = \frac{1}{-5} \cdot \begin{bmatrix} -5 & 3 & 7 \ -1 & 1 & 1 \ 7 & -5 & -5 \end{bmatrix} \cdot \begin{bmatrix} 3 \ -3 \ 4 \end{bmatrix} $$
-
Calculate the product of the matrices ( A^{-1} ) and ( B )
We multiply the inverse matrix ( A^{-1} ) with the matrix ( B ). The multiplication is performed as follows:
- The first element: $(-5)(3) + (3)(-3) + (7)(4) = -15 - 9 + 28 = 4$
- The second element: $(-1)(3) + (1)(-3) + (1)(4) = -3 - 3 + 4 = -2$
- The third element: $(7)(3) + (-5)(-3) + (-5)(4) = 21 + 15 - 20 = 16$
Thus, $$ \begin{bmatrix} 4 \ -2 \ 16 \end{bmatrix} $$
-
Multiply the result by ( \frac{1}{-5} )
Now we scale the resulting matrix by ( \frac{1}{-5} ):
- First element: $$ \frac{4}{-5} = -\frac{4}{5} $$
- Second element: $$ \frac{-2}{-5} = \frac{2}{5} $$
- Third element: $$ \frac{16}{-5} = -\frac{16}{5} $$
Therefore: $$ \begin{bmatrix} -\frac{4}{5} \ \frac{2}{5} \ -\frac{16}{5} \end{bmatrix} $$
-
Final Solution
Thus, the values are:
- ( x = -\frac{4}{5} )
- ( y = \frac{2}{5} )
- ( z = -\frac{16}{5} )
$$ \begin{bmatrix} x \ y \ z \end{bmatrix}
\begin{bmatrix} -\frac{4}{5} \ \frac{2}{5} \ -\frac{16}{5} \end{bmatrix} $$
More Information
The calculations involve multiplying matrices and applying scalar multiplication to the resultant matrix. These steps show how matrix equations can be solved through systematic matrix operations.
Tips
- Error in Matrix Multiplication: Ensure that each element is computed correctly by following the appropriate multiplication rules.
- Neglecting Scalar Multiplication: Remember to apply the scalar multiplication after obtaining the matrix product.
AI-generated content may contain errors. Please verify critical information