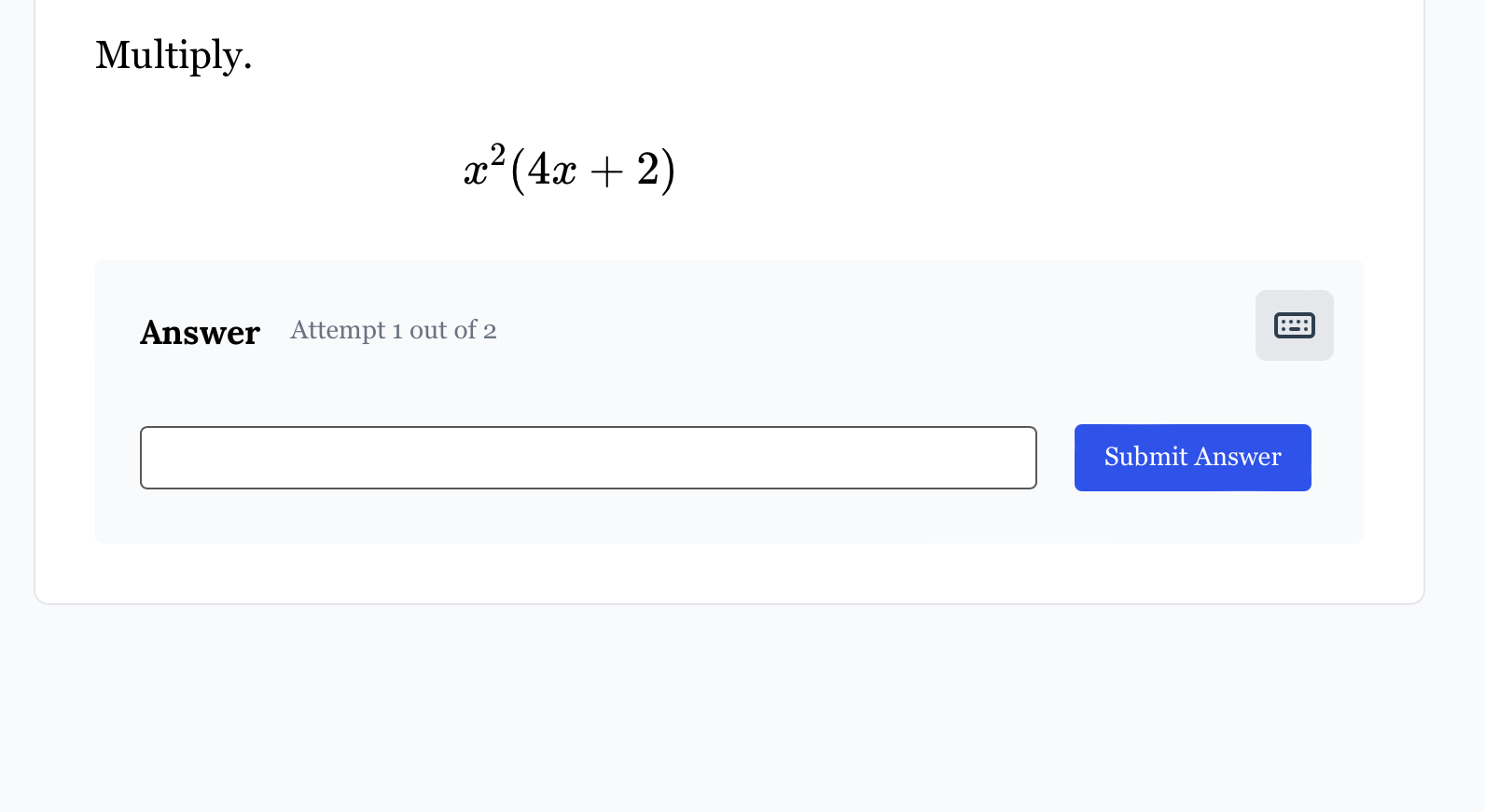
Multiply x²(4x + 2).
Understand the Problem
The question is asking to multiply the polynomial expression x²(4x + 2). The high level approach involves distributing x² to each term inside the parentheses.
Answer
The product is \( 4x^3 + 2x^2 \).
Answer for screen readers
The final answer is ( 4x^3 + 2x^2 ).
Steps to Solve
-
Distribute ( x^2 ) to the first term
Multiply ( x^2 ) by the first term inside the parentheses, ( 4x ): $$ x^2 \cdot 4x = 4x^{2+1} = 4x^3 $$
-
Distribute ( x^2 ) to the second term
Now multiply ( x^2 ) by the second term inside the parentheses, ( 2 ): $$ x^2 \cdot 2 = 2x^2 $$
-
Combine the results
Combine the terms obtained from the distribution: $$ 4x^3 + 2x^2 $$
The final answer is ( 4x^3 + 2x^2 ).
More Information
This result shows that when multiplying a polynomial expression, you distribute each term sequentially and combine like terms if necessary.
Tips
- Forgetting to distribute to all terms in the parentheses.
- Failing to combine like terms once the distribution is complete.
AI-generated content may contain errors. Please verify critical information