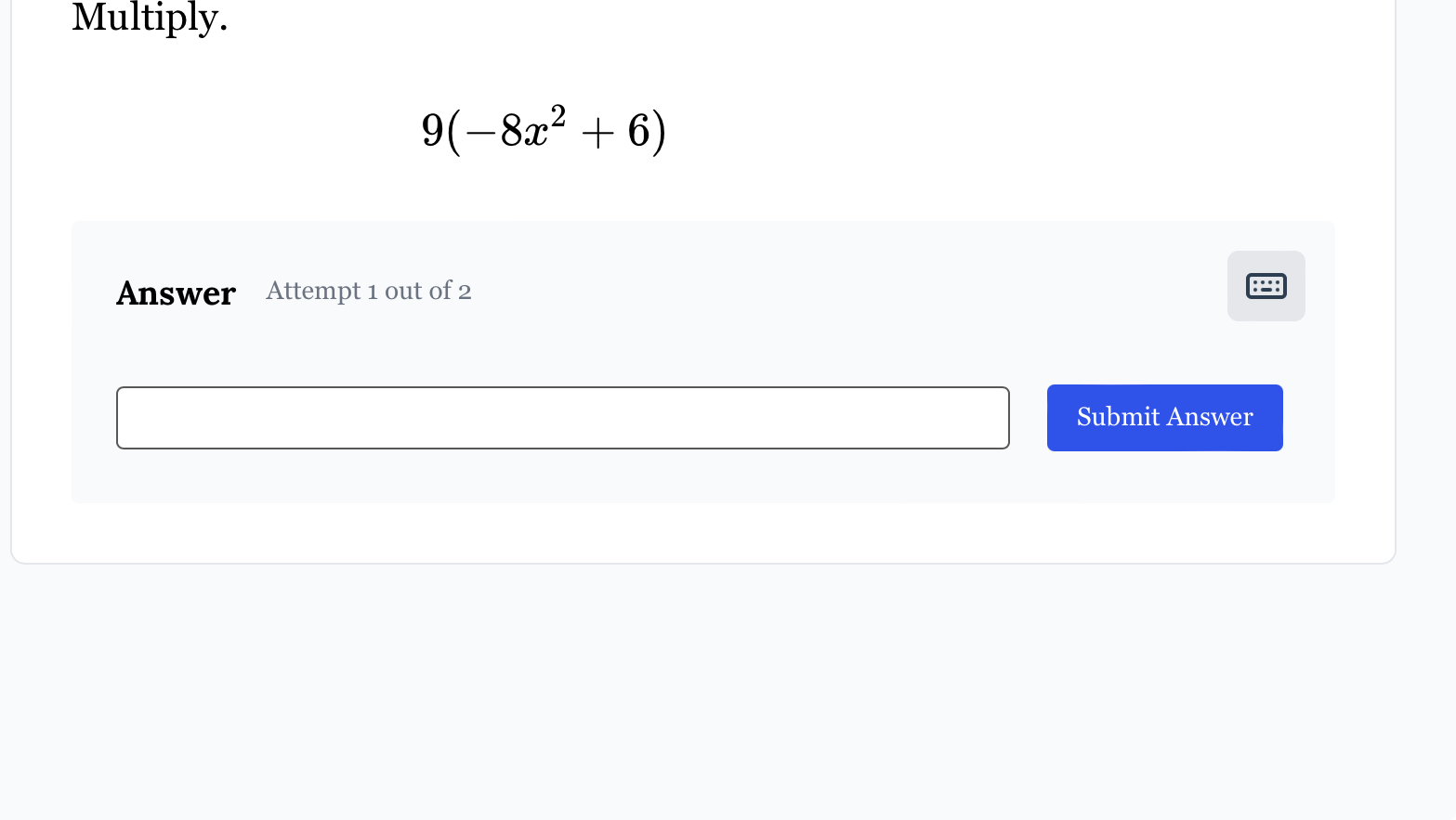
Multiply 9(-8x² + 6).
Understand the Problem
The question is asking to multiply the expression 9(-8x² + 6), which involves applying the distributive property to simplify the expression.
Answer
$-72x^2 + 54$
Answer for screen readers
The final expression is $-72x^2 + 54$.
Steps to Solve
- Apply the Distributive Property
We start by applying the distributive property, which states that $a(b + c) = ab + ac$.
In this case, we multiply 9 by each term inside the parentheses:
$$ 9(-8x^2 + 6) = 9 \cdot (-8x^2) + 9 \cdot 6 $$
- Multiply the First Term
Now, calculate the product of 9 and $-8x^2$:
$$ 9 \cdot (-8x^2) = -72x^2 $$
- Multiply the Second Term
Next, calculate the product of 9 and 6:
$$ 9 \cdot 6 = 54 $$
- Combine the Results
Combine the results from the previous multiplications:
$$ -72x^2 + 54 $$
The final expression is $-72x^2 + 54$.
More Information
This result shows how the distributive property can simplify expressions where a term multiplies a binomial. The coefficients of $x^2$ and the constant term are derived from straightforward multiplications.
Tips
- Forgetting to distribute the multiplier to each term in the parentheses, leading to incorrect results.
- Not paying attention to the signs, which can change the outcome, especially when multiplying negative terms.
AI-generated content may contain errors. Please verify critical information