Multiply $(3\sqrt{2} - 2\sqrt{5})(4\sqrt{2} + 2\sqrt{5})$
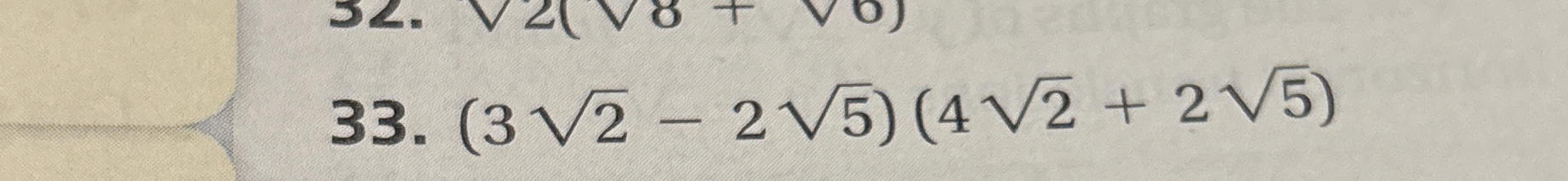
Understand the Problem
The question asks to multiply two binomials that contain radicals. We will use the distributive property (often remembered by the acronym FOIL) to multiply each term in the first binomial by each term in the second binomial, and then we will simplify the result by combining like terms.
Answer
$4 - 2\sqrt{10}$
Answer for screen readers
$4 - 2\sqrt{10}$
Steps to Solve
-
Multiply the first terms Multiply the first terms of each binomial: $3\sqrt{2}$ and $4\sqrt{2}$. $(3\sqrt{2}) \cdot (4\sqrt{2}) = 3 \cdot 4 \cdot \sqrt{2} \cdot \sqrt{2} = 12 \cdot 2 = 24$
-
Multiply the outer terms Multiply the outer terms of the binomials: $3\sqrt{2}$ and $2\sqrt{5}$. $(3\sqrt{2}) \cdot (2\sqrt{5}) = 3 \cdot 2 \cdot \sqrt{2} \cdot \sqrt{5} = 6\sqrt{10}$
-
Multiply the inner terms Multiply the inner terms of the binomials: $-2\sqrt{5}$ and $4\sqrt{2}$. $(-2\sqrt{5}) \cdot (4\sqrt{2}) = -2 \cdot 4 \cdot \sqrt{5} \cdot \sqrt{2} = -8\sqrt{10}$
-
Multiply the last terms Multiply the last terms of each binomial: $-2\sqrt{5}$ and $2\sqrt{5}$. $(-2\sqrt{5}) \cdot (2\sqrt{5}) = -2 \cdot 2 \cdot \sqrt{5} \cdot \sqrt{5} = -4 \cdot 5 = -20$
-
Combine all terms Combine the results from the previous steps. $24 + 6\sqrt{10} - 8\sqrt{10} - 20$
-
Simplify by combining like terms Combine the constant terms $24$ and $-20$, and the terms with $\sqrt{10}$. $24 - 20 + 6\sqrt{10} - 8\sqrt{10} = 4 - 2\sqrt{10}$
$4 - 2\sqrt{10}$
More Information
The simplified form of $(3 \sqrt{2}-2 \sqrt{5})(4 \sqrt{2} + 2 \sqrt{5})$ is $4 - 2\sqrt{10}$.
Tips
A common mistake is incorrectly multiplying or simplifying the radicals. Remember that $\sqrt{a} \cdot \sqrt{b} = \sqrt{ab}$. Also, watch out for the negative signs when multiplying. Failing to combine like terms at the end is another common mistake.
AI-generated content may contain errors. Please verify critical information