Multiple math questions from an image.
Understand the Problem
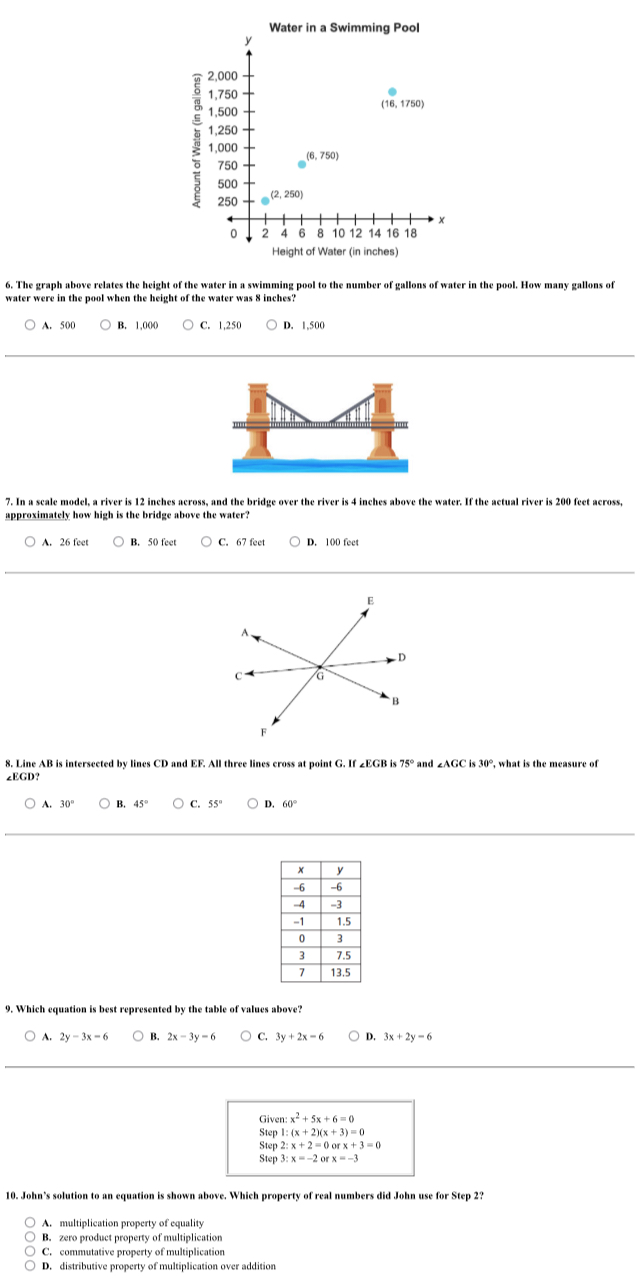
The image contains multiple math questions. Question 6 asks to read a graph relating height of water to gallons, and determine the number of gallons at a specific height. Question 7 involves scaling. Question 8 involves angles. Question 9 involves finding the equation that fits the table. Question 10 involves understanding which property was used in a math problem.
Answer
6. 1,000 7. 67 8. $45^\circ$ 9. $2y - 3x = 6$ 10. zero product property of multiplication
Answer for screen readers
- B. 1,000
- C. 67 feet
- B. 45°
- A. $2y - 3x = 6$
- B. zero product property of multiplication
Steps to Solve
- Question 6: Read the graph
Locate 8 inches on the x-axis (Height of Water). Find the corresponding point on the graph. Estimate the y-axis value (Amount of Water in gallons) for that point. Be careful about the scale of the y-axis.
- Question 7: Set up a proportion
Set up a proportion to relate the scale model to the actual river. We know the river width in the model is 12 inches and in reality is 200 feet. The bridge height in the model is 4 inches. Let $x$ be the bridge height in reality.
$$ \frac{12 \text{ inches (model river)}}{200 \text{ feet (actual river)}} = \frac{4 \text{ inches (model bridge)}}{x \text{ feet (actual bridge)}} $$
- Question 7: Solve the proportion
Solve for $x$:
$$ 12x = 4 \cdot 200 $$ $$ 12x = 800 $$ $$ x = \frac{800}{12} $$ $$ x \approx 66.67 $$
- Question 8: Find $\angle$EGD
We know that $\angle EGB = 75^\circ$ and $\angle AGC = 30^\circ$. Since AB is a line, $\angle AGB = 180^\circ$. Then $\angle EGA = \angle AGB - \angle EGB = 180^\circ - 75^\circ = 105^\circ$. Since CD is a line, $\angle CGD = 180^\circ$. Then $\angle EGD = \angle CGD - \angle CGE$. Also, $\angle CGE = \angle AGC + \angle EGA = 30^\circ + 105^\circ = \angle CGE = 135^\circ \implies \angle CGE = \angle FGA$. Then $\angle DGE = 180^\circ - 135^\circ = 45^\circ$. It's easier to recognise that $\angle EGD$ and $\angle EGB$ and $\angle BGD$ sum up to 180
$\angle EGB$ and $\angle EGA$ are supplementary to $180^\circ$ therefore $\angle EGA = 180 - 75 = 105^\circ$.
Similarly $\angle AGC$ and $\angle BGC$ are supplementary and sum up to $180^\circ$, so $\angle BGC = 180 - 30 = 150^\circ$
$\angle EGB + \angle BGC + \angle CGD + \angle DGE + \angle EGF + \angle FGA + \angle AGC + \angle CGE = 360^\circ$
Furthermore $\angle FGA = \angle CGE$ and $\angle DGE = \angle CGF$, $\angle AGC = \angle FGB$ and $\angle DGB = \angle EGA$
The angle we're looking for $\angle EGD = \angle EGA - \angle DGA = 105 - 60 = 45^\circ$. We have $\angle EGB + \angle BGD = \angle EGA $ $\angle EGB + \angle BGD = 180^\circ $ $\angle EGD = 180 - \angle EGA $
Since $\angle EGB$ and $\angle EGA$ are adjacent and create the line AB, they're supplementary meaning they add up to $180^\circ$: $75 + \angle EGA = 180 \implies \angle EGA = 105^\circ$
Since $\angle AGC$ and $\angle CGB$ are adjacent and create the line AB, they're supplementary meaning they add up to $180^\circ$: $30 + \angle CGB = 180 \implies \angle CGB = 150^\circ$
- Question 9: Test the points
Plug in the x and y values from the table into each equation to see which one holds true for all points.
Let's start with the point (0, 3): A. $2(3) - 3(0) = 6 \implies 6=6$ B. $2(0) - 3(3) = 6 \implies -9 = 6$ (False) C. $3(3) + 2(0) = 6 \implies 9 = 6$ (False) D. $3(0) + 2(3) = 6 \implies 6 = 6$
Now, let's try the point (-1, 1.5) with options A and D: A. $2(1.5) - 3(-1) = 6 \implies 3 + 3 = 6 \implies 6 = 6$ D. $3(-1) + 2(1.5) = 6 \implies -3 + 3 = 6 \implies 0 = 6$ (False)
Since option D is false, option A must be the correct equation
- Question 10: Identify the property
In step 2, John set each factor equal to zero. This utilizes the zero product property.
- B. 1,000
- C. 67 feet
- B. 45°
- A. $2y - 3x = 6$
- B. zero product property of multiplication
More Information
Question 6: The graph may not be perfectly accurate, but 1,000 is the closest answer choice. Question 7: The answer is approximate because we are rounding the result. Question 8: The final angle is fairly intuitive. Question 9: Testing points is a surefire way to arrive at the correct answer. Question 10: Know your algebraic properties!
Tips
Question 6: Misreading the graph or the scale on the y-axis. Double-check the axes and their scales. Question 7: Setting up the proportion incorrectly. Ensure corresponding values are in the correct places in the proportion. Question 8: Incorrectly measuring the angles Question 9: Only verifying one point. Question 10: Confusing the zero product property with other properties.
AI-generated content may contain errors. Please verify critical information