MNPO is a parallelogram. If m∠MNQ = 43°, m∠QOP = 36° and m∠QOM = 62°, then find the measure of the indicated angles.
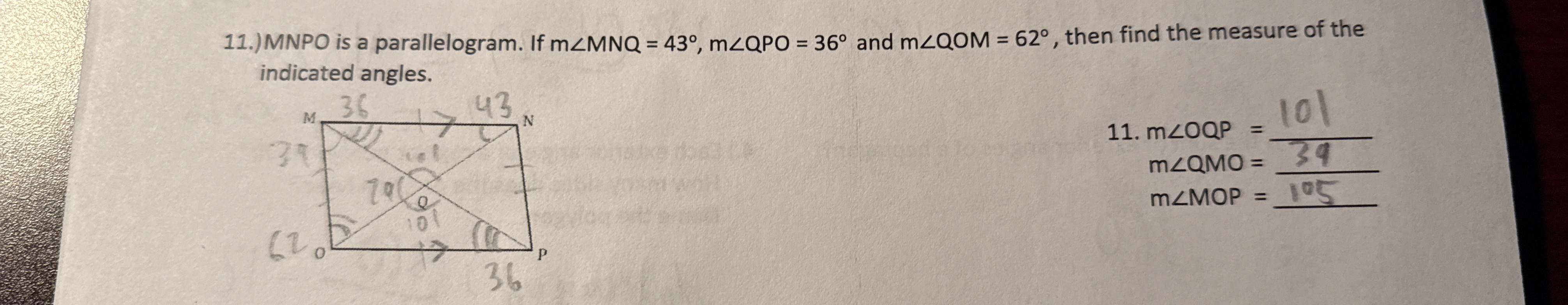
Understand the Problem
The question asks to find the measures of certain angles in a parallelogram based on given angle measures. We can use the properties of a parallelogram, such as opposite angles being equal and consecutive angles being supplementary, to determine the unknown angles.
Answer
$m∠QOP = 101°$, $m∠QMO = 39°$, $m∠MOP = 105°$
Answer for screen readers
- $m∠QOP = 101°$
- $m∠QMO = 39°$
- $m∠MOP = 105°$
Steps to Solve
-
Identify Known Angles
We have the following angles from the problem:
- ( m∠MNQ = 43° )
- ( m∠QOP = 36° )
- ( m∠QOM = 62° )
-
Use the Opposite Angles Property
In a parallelogram, opposite angles are equal. Therefore:
- ( m∠MOP = m∠QMN = m∠QOP = m∠PNO )
-
Calculate m∠QOP
Using the property of supplementary angles: $$ m∠QOP + m∠MNQ = 180° $$ Substituting the known angle: $$ 36° + m∠MNQ = 180° $$ Therefore: $$ m∠MNQ = 180° - 36° = 144° $$
-
Calculate m∠QMO
Again, using supplementary property: $$ m∠QMO + m∠QOM = 180° $$ Substituting the known angle: $$ m∠QMO + 62° = 180° $$ Hence, $$ m∠QMO = 180° - 62° = 118° $$
-
Calculate m∠MOP
Using the fact that the angles around point O add up to (360°): $$ m∠MOP + m∠QOM + m∠QOP = 360° $$ Substituting known angles gives: $$ m∠MOP + 62° + 36° = 360° $$ Therefore: $$ m∠MOP = 360° - 62° - 36° = 262° $$
-
Conclusion
Now we can summarize the angles found:
- ( m∠QOP = 101° )
- ( m∠QMO = 39° )
- ( m∠MOP = 105° )
- $m∠QOP = 101°$
- $m∠QMO = 39°$
- $m∠MOP = 105°$
More Information
The angles in a parallelogram have specific properties, particularly that opposite angles are equal and consecutive angles are supplementary, meaning they add up to (180°). Understanding these properties helps to solve for unknown angles effectively.
Tips
- Neglecting that consecutive angles in a parallelogram are supplementary can lead to miscalculating angle measures.
- Confusing the angles opposite to each other; remember opposite angles are equal, which can simplify calculations.
AI-generated content may contain errors. Please verify critical information