Understand the Problem
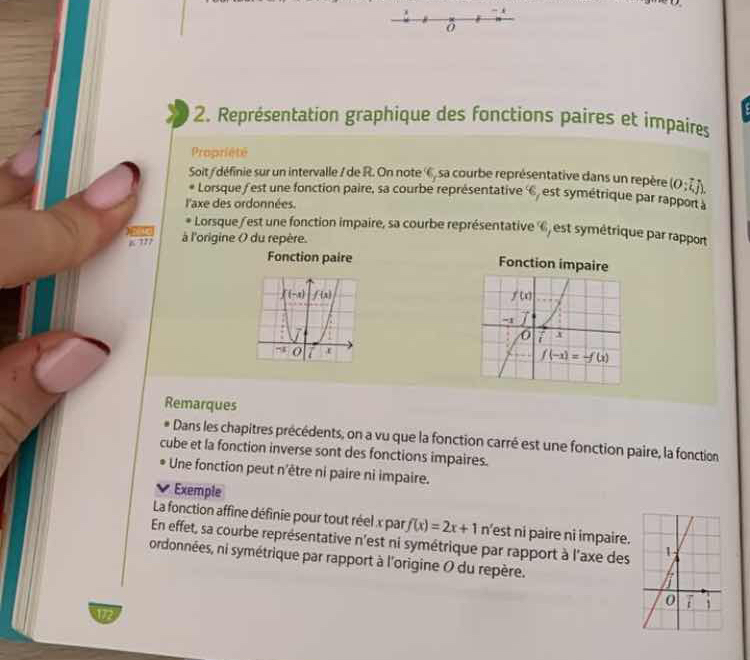
La question aborde la représentation graphique des fonctions paires et impaires en mathématiques, y compris leurs propriétés et des exemples. Elle vise à comprendre comment ces fonctions se comportent graphiquement.
Answer
La fonction $f(x) = 2x + 1$ est ni paire ni impair.
Answer for screen readers
La fonction $f(x) = 2x + 1$ est ni paire ni impair.
Steps to Solve
-
Understanding functions pair and impair
Une fonction est dite paire si $f(-x) = f(x)$ pour tout $x$ dans son domaine. Son graphique est symétrique par rapport à l'axe des ordonnées. Une fonction est dite impair si $f(-x) = -f(x)$. Son graphique est symétrique par rapport à l'origine. -
Analyzing the given function
Pour la fonction $f(x) = 2x + 1$, vérifions d'abord si c'est une fonction paire ou impair en évaluant $f(-x)$: $$ f(-x) = 2(-x) + 1 = -2x + 1 $$ -
Determine symmetry
Comparons $f(-x)$ avec $f(x)$:- Pour la paire: $f(-x) \neq f(x)$
- Pour l'impair: $f(-x) \neq -f(x)$ En effet, $$ -f(x) = - (2x + 1) = -2x - 1 $$
-
Conclusion on the type of function
Puisque ni l'une ni l'autre des conditions n'est satisfaite ($f(-x) \neq f(x)$ et $f(-x) \neq -f(x)$), la fonction $f(x) = 2x + 1$ n'est ni paire ni impair.
La fonction $f(x) = 2x + 1$ est ni paire ni impair.
More Information
Les fonctions paires et impaires sont des concepts importants en mathématiques, en particulier dans l'étude de la symétrie des graphiques. Cette fonction affine a la forme d'une droite, ce qui montre que toutes les droites ne sont pas nécessairement symétriques.
Tips
- Confondre les critères en pensant qu'une fonction pourrait être à la fois paire et impair. Cela n'est pas possible.
- Ne pas vérifier les deux conditions pour déterminer la parité d'une fonction.
AI-generated content may contain errors. Please verify critical information